
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | a<c<b |
分析 在同一坐标系中画出相应函数的图象,数形结合可得答案.
解答 解:∵a,b,c均为正数,且分别为函数$f(x)={2^x}-{log_{\frac{1}{2}}}x$,$g(x)={(\frac{1}{2})^x}-{log_{\frac{1}{2}}}x$,$h(x)={(\frac{1}{2})^x}-{log_{\frac{2}{3}}}x$的零点,
∴a,b,c分别为函数$y={2}^{x}与y=lo{g}_{\frac{1}{2}}x$,函数$y={(\frac{1}{2})}^{x}与y=lo{g}_{\frac{1}{2}}x$,函数$y={(\frac{1}{2})}^{x}与y=lo{g}_{\frac{2}{3}}x$交点的横坐标,
在同一坐标系中画出相应函数的图象,如下图所示: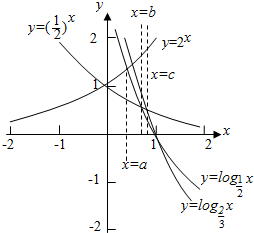
由图可得:a<b<c,
故选:A
点评 本题考查的知识点是函数的零点,数列结合思想,画出满足条件的图象是解答的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com