
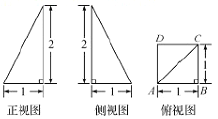
【题目】某四棱锥的三视图如图所示,该四棱锥外接球的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】该四棱锥的底面是正方形,其中一条侧棱与底面垂直,所以该四棱锥的外接球就是它所在的长方体的外接球,半径![]() ,所以体积
,所以体积![]() ,故选D.
,故选D.
(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.
(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.
(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.


科目:高中数学 来源: 题型:
【题目】某单位附近只有甲、乙两个临时停车场,它们各有![]() 个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
个车位,为了方便市民停车,某互联网停车公司对这两个停车场,在某些固定时刻的剩余停车位进行记录,如下表:
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的![]() ,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
,那么当车主驱车抵达单位附近时,该公司将会向车主发出停车场饱和警报.
(1)假设某车主在以上六个时刻抵达单位附近的可能性相同,求他收到甲停车场饱和警报的概率;
(2)从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率;
(3)当乙停车场发出饱和警报时,求甲停车场也发出饱和警报的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)抛物线的顶点在原点,坐标轴为对称轴,并经过点![]() ,求此抛物线的方程.
,求此抛物线的方程.
(Ⅱ)已知圆: ![]() (
(![]() ),把圆上的各点纵坐标不变,横坐标伸长到原来的
),把圆上的各点纵坐标不变,横坐标伸长到原来的![]() 倍得一椭圆.求椭圆方程,并证明椭圆离心率是与
倍得一椭圆.求椭圆方程,并证明椭圆离心率是与![]() 无关的常数.
无关的常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,函数
,函数![]() ,
, ![]() .
.
(Ⅰ)若![]() 与
与![]() 有公共点
有公共点![]() ,且在
,且在![]() 点处切线相同,求该切线方程;
点处切线相同,求该切线方程;
(Ⅱ)若函数![]() 有极值但无零点,求实数
有极值但无零点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() ,
, ![]() 时,求
时,求![]() 在区间
在区间![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
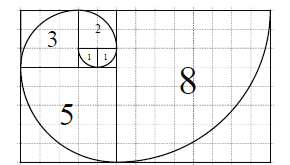
【题目】斐波那契数列![]() 满足:
满足: ![]() .若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前
.若将数列的每一项按照下图方法放进格子里,每一小格子的边长为1,记前![]() 项所占的格子的面积之和为
项所占的格子的面积之和为![]() ,每段螺旋线与其所在的正方形所围成的扇形面积为
,每段螺旋线与其所在的正方形所围成的扇形面积为![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
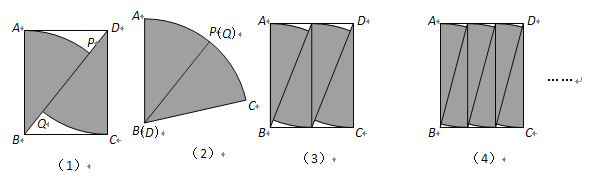
【题目】矩形纸片ABCD中,AB=10cm,BC=8cm.将其按图(1)的方法分割,并按图(2)的方法焊接成扇形;按图(3)的方法将宽BC ![]() 等分,把图(3)中的每个小矩形按图(1)分割并把4个小扇形焊接成一个大扇形;按图(4)的方法将宽BC
等分,把图(3)中的每个小矩形按图(1)分割并把4个小扇形焊接成一个大扇形;按图(4)的方法将宽BC ![]() 等分,把图(4)中的每个小矩形按图(1)分割并把6个小扇形焊接成一个大扇形;……;依次将宽BC
等分,把图(4)中的每个小矩形按图(1)分割并把6个小扇形焊接成一个大扇形;……;依次将宽BC ![]() 等分,每个小矩形按图(1)分割并把
等分,每个小矩形按图(1)分割并把![]() 个小扇形焊接成一个大扇形.当n
个小扇形焊接成一个大扇形.当n![]() 时,最后拼成的大扇形的圆心角的大小为 ( )
时,最后拼成的大扇形的圆心角的大小为 ( )
A. 小于![]() B. 等于
B. 等于![]() C. 大于
C. 大于![]() D. 大于
D. 大于![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com