
【题目】求最大实数![]() ,使得对任意
,使得对任意![]() 阶简单图
阶简单图![]() ,有不等式
,有不等式![]() ,其中,
,其中,![]() 为图
为图![]() 的边数,
的边数,![]() 为图
为图![]() 中三角形的个数.
中三角形的个数.
【答案】![]()
【解析】
先证明一个引理.
引理 设![]() 阶简单图有
阶简单图有![]() 条边,
条边,![]() 个三角形.则
个三角形.则![]() .
.
证明 因为![]() 阶简单图中,
阶简单图中,![]() 个三角形共有
个三角形共有![]() 条边,且每条边至多出现在
条边,且每条边至多出现在![]() 个三角形当中,所以,
个三角形当中,所以,![]() .
.
回到原题.
首先考虑特殊的![]() 阶完全图,有
阶完全图,有![]() .
.
令![]() ,则
,则![]() .
.
下面用数学归纳法证明:![]() 对任意
对任意![]() 阶简单图
阶简单图![]() 成立.
成立.
当![]() 时,结论显然成立.
时,结论显然成立.
假设当![]() 时,结论成立.
时,结论成立.
当![]() 时,取
时,取![]() 为
为![]() 阶简单图中度数最小的顶点,设其度数为
阶简单图中度数最小的顶点,设其度数为![]() ,并设余下的
,并设余下的![]() 个点构成的简单图中有
个点构成的简单图中有![]() 条边,
条边,![]() 个三角形.则由引理知
个三角形.则由引理知![]() .①
.①
由归纳假设知![]() .②
.②
因为点![]() 度数最小,所以,
度数最小,所以,![]() .③
.③
设与点![]() 相邻的
相邻的![]() 个顶点之间连有
个顶点之间连有![]() 条边,这
条边,这![]() 条边每条和点
条边每条和点![]() 都形成一个三角形.故只需证明
都形成一个三角形.故只需证明
![]() . ④
. ④
易知,![]() ,
,![]() .⑤
.⑤
因此,![]() .
.
将式①、③代入上式得![]() .⑥
.⑥
又由式⑤知![]() .⑦
.⑦
由式②、⑥、⑦知式④成立,即当![]() 时,结论成立.
时,结论成立.
从而,对所有![]() ,结论成立.
,结论成立.
因此,![]() .
.


科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2013位来自不同国家的代表参加一个会议,每位代表都懂得若干种语言,已知其中任意四位代表之间都可进行交谈而不需要此四位代表以外的其他人帮助,即此四人中的任意两人都能讲同一种语言而实现直接沟通,或者通过第三个人的翻译实现间接沟通,或者通过他们各自的翻译能讲的同一种语言实现低效的间接沟通,证明:可以将所有代表分配住进671个房间,每个房间住3人,使得每个房间的3人都可以交谈。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从左到右依次写出1到10000的全部正整数,然后去掉那些能被5或7整除的数,将剩下的数连成一排组成一个新数。试求:
(1)新数的位数;
(2)新数被11除的余数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市移动公司为了提高服务质量,决定对使用A,B两种套餐的集团用户进行调查,准备从本市![]() 个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为
个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为![]() .
.
![]() 求n的值;
求n的值;
![]() 若取出的2个集团是同一类集团,求全为大集团的概率;
若取出的2个集团是同一类集团,求全为大集团的概率;
![]() 若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为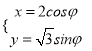 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年3月,各行各业开始复工复产,生活逐步恢复常态,某物流公司承担从甲地到乙地的蔬菜运输业务.已知该公司统计了往年同期200天内每天配送的蔬菜量X(40≤X<200,单位:件.注:蔬菜全部用统一规格的包装箱包装),并分组统计得到表格如表:
蔬菜量X | [40,80) | [80,120) | [120,160) | [160,200) |
天数 | 25 | 50 | 100 | 25 |
若将频率视为概率,试解答如下问题:
(1)该物流公司负责人决定随机抽出3天的数据来分析配送的蔬菜量的情况,求这3天配送的蔬菜量中至多有2天小于120件的概率;
(2)该物流公司拟一次性租赁一批货车专门运营从甲地到乙地的蔬菜运输.已知一辆货车每天只能运营一趟,每辆货车每趟最多可装载40件,满载才发车,否则不发车.若发车,则每辆货车每趟可获利2000元;若未发车,则每辆货车每天平均亏损400元.为使该物流公司此项业务的营业利润最大,该物流公司应一次性租赁几辆货车?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com