
【题目】设实数a∈R,函数 ![]() 是R上的奇函数. (Ⅰ)求实数a的值;
是R上的奇函数. (Ⅰ)求实数a的值;
(Ⅱ)当x∈(1,1)时,求满足不等式f(1m)+f(1m2)<0的实数m的取值范围.
【答案】解:(Ⅰ)因为函数 ![]() 是R上的奇函数,所以f(0)=0.
是R上的奇函数,所以f(0)=0.
即 ![]() ,解得a=1.(3分)
,解得a=1.(3分)
(Ⅱ)由(Ⅰ),得 ![]() .
.
因为f(x)是R上的奇函数,由f(1m)+f(1m2)<0,
得f(1m)<f(1m2),即f(1m)<f(m21).
下面证明f(x)在R是增函数.
设x1,x2∈R且x1<x2,则 
因为x1<x2,所以 ![]() ,
, ![]() ,而
,而 ![]() ,
,
所以  ,
,
即f(x1)<f(x2),所以 ![]() 是R上的增函数.
是R上的增函数.
当x∈(1,1)时,由f(1m)<f(m21)得  ,
,
解得 ![]() .
.
所以,当x∈(1,1)时,满足不等式f(1m)+f(1m2)<0的实数m的取值范围是 ![]() .
.
【解析】(Ⅰ)根据函数奇偶性的定义求出a的值即可,(Ⅱ)根据条件判断函数的单调性,利用函数奇偶性和单调性的性质进行转化求解即可.
【考点精析】本题主要考查了奇偶性与单调性的综合的相关知识点,需要掌握奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知倾斜角60°为的直线l平分圆:x2+y2+2x+4y﹣4=0,则直线l的方程为( )
A.![]() x﹣y+
x﹣y+ ![]() +2=0
+2=0
B.![]() x+y+
x+y+ ![]() +2=0
+2=0
C.![]() x﹣y+
x﹣y+ ![]() ﹣2=0
﹣2=0
D.![]() x﹣y﹣
x﹣y﹣ ![]() +2=0
+2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.奇函数f(x)的图象经过(0,0)点
B.y=|x+1|+|x﹣1|(x∈(﹣4,4])是偶函数
C.幂函数y=x ![]() 过(1,1)点
过(1,1)点
D.y=sin2x(x∈[0,5π])是以π为周期的函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的程序框图所表示的算法功能是输出( ) 
A.使1×2×4×6××n≥2017成立的最小整数n
B.使1×2×4×6××n≥2017成立的最大整数n
C.使1×2×4×6××n≥2017成立的最小整数n+2
D.使1×2×4×6××n≥2017成立的最大整数n+2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定圆C:x2+(y﹣3)2=4,定直线m;x+3y+6=0,过A(﹣1,0)的一条动直线l与直线相交于N,与圆C相交于P,Q两点,
(1)当l与m垂直时,求出N点的坐标,并证明:l过圆心C;
(2)当|PQ|=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知R(x0 , y0)是椭圆C: ![]() =1上的一点,从原点O向圆R:(x﹣x0)2+(y﹣y0)2=8作两条切线,分别交椭圆于点P,Q.
=1上的一点,从原点O向圆R:(x﹣x0)2+(y﹣y0)2=8作两条切线,分别交椭圆于点P,Q. 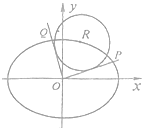
(1)若R点在第一象限,且直线OP,OQ互相垂直,求圆R的方程;
(2)若直线OP,OQ的斜率存在,并记为k1 , k2 , 求k1k2的值;
(3)试问OP2+OQ2是否为定值?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M的圆心在直线x﹣2y+4=0上,且与x轴交于两点A(﹣5,0),B(1,0). (Ⅰ)求圆M的方程;
(Ⅱ)求过点C(1,2)的圆M的切线方程;
(Ⅲ)已知D(﹣3,4),点P在圆M上运动,求以AD,AP为一组邻边的平行四边形的另一个顶点Q轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额的商品后即可参加抽奖,抽奖有两种方案可供选择. 方案一:从装有4个红球和2个白球的不透明箱中,随机摸出2个球,若摸出的2个球都是红球则中奖,否则不中奖;
方案二:掷2颗骰子,如果出现的点数至少有一个为4则中奖,否则不中奖.(注:骰子(或球)的大小、形状、质地均相同)
(Ⅰ)有顾客认为,在方案一种,箱子中的红球个数比白球个数多,所以中奖的概率大于 ![]() .你认为正确吗?请说明理由;
.你认为正确吗?请说明理由;
(Ⅱ)如果是你参加抽奖,你会选择哪种方案?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com