
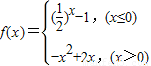 ,对于下列命题:
,对于下列命题: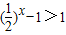 ,解出即可判断③的对错;
,解出即可判断③的对错;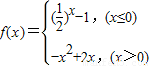 ,显然函数y=|f(x)|的图象不为轴对称图形.
,显然函数y=|f(x)|的图象不为轴对称图形.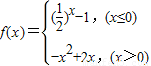 ,
,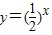 下移1个单位得到的;
下移1个单位得到的;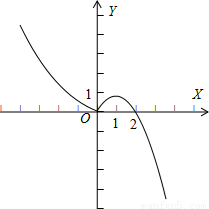
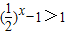 ,解得x<-1,故③对;
,解得x<-1,故③对;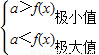 ,
,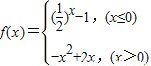 ,显然函数y=|f(x)|的图象不为轴对称图形,故⑤为假命题.
,显然函数y=|f(x)|的图象不为轴对称图形,故⑤为假命题.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知函数![]() .
.
对于下列命题:
① 函数![]() 是周期函数;
是周期函数;
② 函数![]() 既有最大值又有最小值;
既有最大值又有最小值;
③ 函数![]() 的定义域是R,且其图象有对称轴;
的定义域是R,且其图象有对称轴;
④ 对于任意![]() (
(![]() 是函数
是函数![]() 的导函数).
的导函数).
其中真命题的序号是 .(填写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省马鞍山高三三模文科数学试卷(解析版) 题型:填空题
已知函数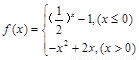 ,对于下列命题:
,对于下列命题:
①函数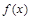 的最小值是0;
的最小值是0;
②函数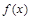 在
在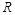 上是单调递减函数;
上是单调递减函数;
③若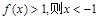 ;
;
④若函数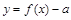 有三个零点,则
有三个零点,则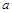 的取值范围是
的取值范围是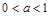 ;
;
⑤函数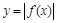 关于直线
关于直线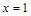 对称.
对称.
其中正确命题的序号是____________________.(填上你认为所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高二下第三次(期末)质检文科数学卷(解析版) 题型:填空题
已知函数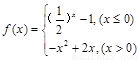 ,对于下列命题:
,对于下列命题:
①函数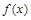 的最小值是0;
的最小值是0;
②函数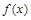 在
在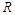 上是单调递减函数;
上是单调递减函数;
③若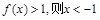 ;
;
④若函数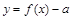 有三个零点,则
有三个零点,则 的取值范围是
的取值范围是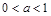 ;
;
⑤函数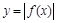 关于直线
关于直线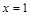 对称.
对称.
其中正确命题的序号是______.(填上你认为所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源:正定中学2010高三下学期第一次考试(数学理) 题型:填空题
已知函数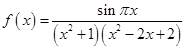 .
.
对于下列命题:
① 函数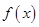 是周期函数;
是周期函数;
② 函数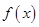 既有最大值又有最小值;
既有最大值又有最小值;
③ 函数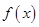 的定义域是R,且其图象有对称轴;
的定义域是R,且其图象有对称轴;
④ 对于任意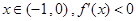 (
(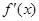 是函数
是函数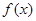 的导函数).
的导函数).
其中真命题的序号是 .(填写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源:2010-2011年广东省佛山市高一上学期期中考试数学试卷 题型:填空题
已知函数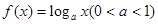 ,对于下列命题:
,对于下列命题:
①若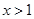 ,则
,则 ; ②若
; ②若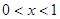 ,则
,则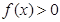 ;
;
③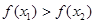 ,则
,则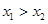 ; ④
; ④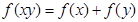 .
.
其中正确的命题的序号是 (写出所有正确命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com