

 .
.
 ,其中n=a+b+c+d)
,其中n=a+b+c+d)科目:高中数学 来源:不详 题型:解答题
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
 ;
; ,
, )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
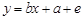 中,下列说法正确的是( )
中,下列说法正确的是( )A.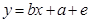 是一次函数 是一次函数 |
B.因变量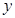 是由自变量 是由自变量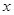 唯一确定的 唯一确定的 |
C.因变量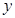 除了受自变量 除了受自变量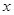 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差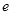 的产生 的产生 |
D.随机误差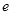 是由于计算不准确造成的,可以通过精确计算避免随机误差 是由于计算不准确造成的,可以通过精确计算避免随机误差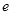 的产生 的产生 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
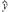 =
= x+
x+ ,求得
,求得 =0.51,
=0.51, =61.75,
=61.75, =38.14,则线性回归方程为( )
=38.14,则线性回归方程为( )A.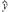 =0.51x+6.65 =0.51x+6.65 | B.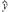 =6.65x+0.51 =6.65x+0.51 |
C.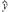 =0.51x+42.30 =0.51x+42.30 | D.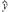 =42.30x+0.51 =42.30x+0.51 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 =0.85x-85.7,则在样本点(165,57)处的残差为( )
=0.85x-85.7,则在样本点(165,57)处的残差为( )| A.54.55 | B.2.45 | C.3.45 | D.111.55 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
 =-3.2x+
=-3.2x+ 则实数
则实数 的值是________.
的值是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①② | B.②③ | C.①③ | D.①②③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | y1 | y2 | 总计 |
| x1 | a | 21 | 73 |
| x2 | 22 | 25 | 47 |
| 总计 | b | 46 | 120 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com