
【题目】在平面直角坐标中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为ρsin2θ=2acosθ(a>0),直线l的参数方程为 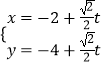 (t为参数),直线l与曲线C相交于A,B两点.
(t为参数),直线l与曲线C相交于A,B两点.
(1)写出曲线C的直角坐标方程和直线l的普通方程;
(2)若|AB|=2 ![]() ,求a的值.
,求a的值.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】对于下列四个命题
p1:x0∈(0,+∞),( ![]() )x0<(
)x0<( ![]() )x0
)x0
p2:x0∈(0,1), ![]() x0>
x0> ![]() x0
x0
p3:x∈(0,+∞),( ![]() )x>
)x> ![]() x
x
p4:x∈(0, ![]() ),(
),( ![]() )x<
)x< ![]() x.
x.
其中的真命题是( )
A.p1 , p3
B.p1 , p4
C.p2 , p3
D.p2 , p4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)+1(ω>0,|φ|≤ ![]() ),其图象与直线y=﹣1相邻两个交点的距离为π,若f(x)>1对x∈(﹣
),其图象与直线y=﹣1相邻两个交点的距离为π,若f(x)>1对x∈(﹣ ![]() ,
, ![]() )恒成立,则φ的取值范围是( )
)恒成立,则φ的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex+ax+b(a,b∈R)在x=ln2处的切线方程为y=x﹣2ln2. (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若k为差数,当x>0时,(k﹣x)f'(x)<x+1恒成立,求k的最大值(其中f'(x)为f(x)的导函数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别是a,b,c,且 ![]() acosC=(2b﹣
acosC=(2b﹣ ![]() c)cosA.
c)cosA.
(1)求角A的大小;
(2)求cos( ![]() ﹣B)﹣2sin2
﹣B)﹣2sin2 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用 ![]() (单位:元)关于月用电量
(单位:元)关于月用电量 ![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的占80%,求 ![]() 的值;
的值;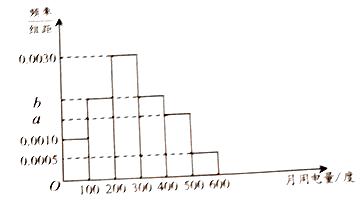
(3)在满足(2)的条件下,估计1月份该市居民用户平均用电费用(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=sinxcosx﹣sin2(x﹣ ![]() ). (Ⅰ)求函数f(x)的最小正周期;
). (Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)求函数f(x﹣ ![]() )在[0,
)在[0, ![]() ]上的最大值与最小值.
]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线C1:  ( t 为参数),曲线C2:
( t 为参数),曲线C2: ![]() (r>0,θ为参数).
(r>0,θ为参数).
(1)当r=1时,求C 1 与C2的交点坐标;
(2)点P 为曲线 C2上一动点,当r= ![]() 时,求点P 到直线C1距离最大时点P 的坐标.
时,求点P 到直线C1距离最大时点P 的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com