
已知椭圆方程为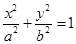 (
(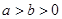 ),F
),F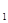 (-c,0)和F
(-c,0)和F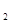 (c,0)分别是椭圆的左 右焦点.
(c,0)分别是椭圆的左 右焦点.
①若P是椭圆上的动点,延长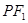 到M,使
到M,使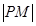 =
=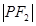 ,则M的轨迹是圆;
,则M的轨迹是圆;
②若P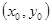 是椭圆上的动点,则
是椭圆上的动点,则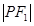
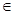
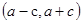 ;
;
③以焦点半径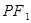 为直径的圆必与以长轴为直径的圆内切;
为直径的圆必与以长轴为直径的圆内切;
④若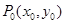 在椭圆
在椭圆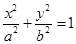 上,则过
上,则过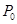 的椭圆的切线方程是
的椭圆的切线方程是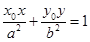 ;
;
⑤点P为椭圆上任意一点 ,则椭圆的焦点角形的面积为
,则椭圆的焦点角形的面积为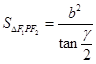 .
.
以上说法中,正确的有
①③④
解析试题分析:根据已知中椭圆方程为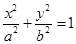 (
(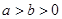 ),F
),F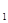 (-c,0)和F
(-c,0)和F (c,0)分别是椭圆的左、右焦点,
(c,0)分别是椭圆的左、右焦点,
因此可知,当满足延长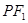 到M,使
到M,使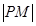 =
=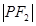 时,则点M的轨迹就是一个圆,故命题1正确
时,则点M的轨迹就是一个圆,故命题1正确
对于命题2,P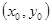 是椭圆上的动点,则
是椭圆上的动点,则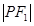
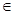
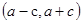 ,不符合两点的距离公式,可以结合函数来得到端点值成立,因此为闭区间,所以错误。
,不符合两点的距离公式,可以结合函数来得到端点值成立,因此为闭区间,所以错误。
命题3中,以焦点半径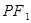 为直径的圆必与以长轴为直径的圆内切;这是利用了两圆的位置关系来判定其结论,成立。
为直径的圆必与以长轴为直径的圆内切;这是利用了两圆的位置关系来判定其结论,成立。
命题4中,点在椭圆上,结合导数的几何意义表示出斜率,那么可知其切线方程为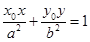 成立。
成立。
命题5中,焦点三角形的面积公式,结合定义和余弦定理可知结论为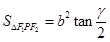 ,因此错误,故填写①③④
,因此错误,故填写①③④
考点:本试题考查了椭圆的方程与性质。
点评:对于椭圆中的定义和性质,以及其切线方程的求解,都可以借助于圆的思想来得到,找到切点,切线的斜率,结合点斜式方程来得到结论。属于中档题。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com