
【题目】设椭圆![]() 的左焦点为
的左焦点为![]() ,离心率为
,离心率为![]() ,椭圆与
,椭圆与![]() 轴与左焦点与点
轴与左焦点与点![]() 的距离为
的距离为![]() .
.
(1)求椭圆方程;
(2)过点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,当
,当![]() 面积为
面积为![]() 时,求
时,求![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)依题意有![]() ,由此解得
,由此解得![]() ,椭圆方程为
,椭圆方程为![]() ;(2)设出直线方程,联立直线方程和椭圆方程,写出韦达定理,求出弦长
;(2)设出直线方程,联立直线方程和椭圆方程,写出韦达定理,求出弦长![]() 关于斜率的表达式,利用点到直线的距离公式求得三角形的高,然后利用三角形面积建立方程,求得斜率
关于斜率的表达式,利用点到直线的距离公式求得三角形的高,然后利用三角形面积建立方程,求得斜率![]() 的值,代入
的值,代入![]() 的表达式,从而求得弦长
的表达式,从而求得弦长![]() .
.
试题解析:
(1)由题意可得![]() ,又
,又![]() ,解得
,解得![]() ,
,
所以椭圆方程为![]() ........................4分
........................4分
(2)根据题意可知,直线![]() 的斜率存在,故设直线
的斜率存在,故设直线![]() 的方程为
的方程为![]() ,设
,设![]() 由方程组
由方程组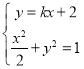 消去
消去![]() 得关于
得关于![]() 的方程
的方程![]() ,.............6分
,.............6分
由直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,则有
两点,则有![]() ,即
,即![]() ,
,
得:![]() ,由根与系数的关系得
,由根与系数的关系得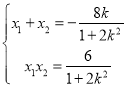 ,
,
故![]() ,.....................8分
,.....................8分
又因为原点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
故![]() 的面积
的面积![]() ,................10分
,................10分
由![]() ,得
,得![]() ,此时
,此时![]() .............................12分
.............................12分


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组![]() ,第二组
,第二组![]() ,…,第五组
,…,第五组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
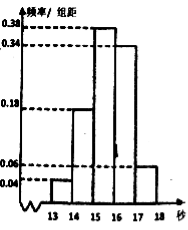
(1)请根据频率分布直方图估计该组数据的众数和中位数(精确到0.1);
(2)从成绩介于![]() 和
和![]() 两组的人中任取2人,求两人分布来自不同组的概率.
两组的人中任取2人,求两人分布来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)2lnx,a∈R.
(I)若x=e是y=f(x)的极值点,求实数a的值;
(Ⅱ)若函数y=f(x)﹣4e2只有一个零点,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,租车已经成为新一代的流行词,租车自驾游也慢慢流行起来,某小车租车点的收费标准是,不超过2天按照300元计算;超过两天的部分每天收费标准为100元(不足1天的部分按1天计算).有甲乙两人相互独立来该租车点租车自驾游(各租一车一次),设甲、乙不超过2天还车的概率分别为![]() ;2天以上且不超过3天还车的概率分别
;2天以上且不超过3天还车的概率分别![]() ;两人租车时间都不会超过4天.
;两人租车时间都不会超过4天.
(1)求甲所付租车费用大于乙所付租车费用的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com