
【题目】已知不等式|x+3|<2x+1的解集为{x|x>m}.
(1)求m的值;
(2)设关于x的方程|x﹣t|+|x+ ![]() |=m(t≠0)有解,求实数t的值.
|=m(t≠0)有解,求实数t的值.
【答案】
(1)解:由不等式|x+3|<2x+1,
可得 ![]() 或
或 ![]() ,
,
解得x>2.
依题意m=2.
(2)解:∵|x﹣t|+|x+ ![]() |≥
|≥ ![]() =
= ![]() =|t|+
=|t|+ ![]() ,
,
当且仅当(x﹣t) ![]() =0时取等号,
=0时取等号,
∵关于x的方程|x﹣t|+|x+ ![]() |=m(t≠0)有解,
|=m(t≠0)有解,
|t|+ ![]() ≥2,
≥2,
另一方面,|t|+ ![]() =2,
=2,
∴|t|+ ![]() =2,
=2,
解得t=±1.
【解析】(1)由不等式|x+3|<2x+1,可得 ![]() 或
或 ![]() ,解出即可得出.(2)由于|x﹣t|+|x+
,解出即可得出.(2)由于|x﹣t|+|x+ ![]() |≥
|≥ ![]() =
= ![]() =|t|+
=|t|+ ![]() ,已知关于x的方程|x﹣t|+|x+
,已知关于x的方程|x﹣t|+|x+ ![]() |=m(t≠0)有解,|t|+
|=m(t≠0)有解,|t|+ ![]() ≥2,另一方面,|t|+
≥2,另一方面,|t|+ ![]() =2,即可得出.
=2,即可得出.
【考点精析】本题主要考查了绝对值不等式的解法的相关知识点,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mex+x2+nx,{x|f(x)=0}={x|f(f(x))=0}≠,则m+n的取值范围为( )
A.(0,4)
B.[0,4)
C.[0,4]
D.(4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
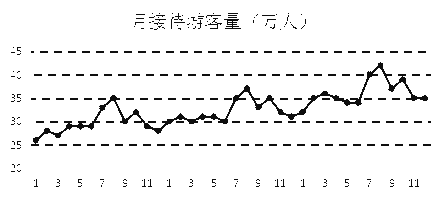
2014年 2015年 2016年
根据该折线图,下列结论错误的是( )
A. 年接待游客量逐年增加
B. 月接待游客量逐月增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点C在椭圆M: ![]() =1(a>b>0)上,若点A(﹣a,0),B(0,
=1(a>b>0)上,若点A(﹣a,0),B(0, ![]() ),且
),且 ![]() =
= ![]()
![]() .
.
(1)求椭圆M的离心率;
(2)设椭圆M的焦距为4,P,Q是椭圆M上不同的两点.线段PQ的垂直平分线为直线l,且直线l不与y轴重合.
①若点P(﹣3,0),直线l过点(0,﹣ ![]() ),求直线l的方程;
),求直线l的方程;
②若直线l过点(0,﹣1),且与x轴的交点为D.求D点横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() 与常数
与常数![]() ,若
,若![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的一个“P数对”,设函数
的一个“P数对”,设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 。
。
(1)若![]() 是
是![]() 的一个“P数对”,且
的一个“P数对”,且![]() ,求常数
,求常数![]() 的值;
的值;
(2)若(1,1)是![]() 的一个“P数对”,且
的一个“P数对”,且![]() 在
在![]() 上单调递增,求函数
上单调递增,求函数![]() 在
在![]() 上的最大值与最小值;
上的最大值与最小值;
(3)若(-2,0)是![]() 的一个“P数对”,且当
的一个“P数对”,且当![]() 时,
时,![]() ,求k的值及
,求k的值及![]() 在区间
在区间![]() 上的最大值与最小值。
上的最大值与最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域是R,对于任意实数
的定义域是R,对于任意实数![]() ,恒有
,恒有![]() ,且当
,且当![]() 时,
时, ![]() 。
。
(1)求证: ![]() ,且当
,且当![]() 时,有
时,有![]() ;
;
(2)判断![]() 在R上的单调性;
在R上的单调性;
(3)设集合A=![]() ,B=
,B=![]() ,若A∩B=
,若A∩B=![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com