
【题目】已知函数![]() ,若
,若![]() (
(![]() ),
),![]() ,
,![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
设x2>x1![]() 4,将已知
4,将已知![]() 转为f(x2)+2mx2>f(x1)+2mx1恒成立,构造函数g(x)=f(x)+2mx,由函数单调性定义可知函数g(x)在[4,+∞)上的单调性,由单调性可求得a的取值范围.
转为f(x2)+2mx2>f(x1)+2mx1恒成立,构造函数g(x)=f(x)+2mx,由函数单调性定义可知函数g(x)在[4,+∞)上的单调性,由单调性可求得a的取值范围.
由已知不妨设x2>x1![]() 4,要
4,要![]() 恒成立,只需f(x2)+2mx2>f(x1)+2mx1,令g(x)=f(x)+2mx,即g(x2)>g(x1),由函数单调性的定义可知g(x)在[4,+∞)上单调递增.又函数g(x)=
恒成立,只需f(x2)+2mx2>f(x1)+2mx1,令g(x)=f(x)+2mx,即g(x2)>g(x1),由函数单调性的定义可知g(x)在[4,+∞)上单调递增.又函数g(x)=![]() ,g'(x)=2x+
,g'(x)=2x+![]() +2m,
+2m,
即g'(x)≥0在[4,+∞)恒成立,即x+![]() +m≥0在[4,+∞)恒成立,
+m≥0在[4,+∞)恒成立,
变量分离得-m![]() x+
x+![]() ,令h(x)= x+
,令h(x)= x+![]() ,只需-m
,只需-m![]()
![]() ,
,
又h(x)在[4,+∞)上单调递增,则![]() =h(4)=4+
=h(4)=4+![]() ,所以-m
,所以-m![]() 4+
4+![]() ,
,
由已知![]() 使-m
使-m![]() 4+
4+![]() 成立,即
成立,即![]() ,
,
即![]() ,
,
故选:D.


科目:高中数学 来源: 题型:
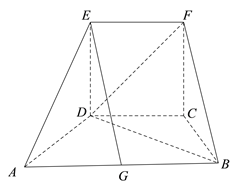
【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.
(Ⅰ)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某环线地铁按内、外环线同时运行,内、外环线的长均为30千米(忽略内、外环线长度差异).
(1)当9列列车同时在内环线上运行时,要使内环线乘客最长候车时间为10分钟,求内环线列车的最小平均速度;
(2)新调整的方案要求内环线列车平均速度为25千米/小时,外环线列车平均速度为30千米/小时.现内、外环线共有18列列车全部投入运行,要使内外环线乘客的最长候车时间之差不超过1分钟,向内、外环线应各投入几列列车运行?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列出了如表并给出了部分数据:
在某一个周期内的图象时,列出了如表并给出了部分数据:
| 0 |
| π |
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请根据上表数据,写出函数![]() 的解析式;(直接写出结果即可)
的解析式;(直接写出结果即可)
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)设![]() ,已知函数
,已知函数![]() 在区间
在区间![]() 上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数
上的最大值是img src="http://thumb.zyjl.cn/questionBank/Upload/2020/11/26/20/139c9676/SYS202011262014544768390673_ST/SYS202011262014544768390673_ST.013.png" width="24" height="24" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,求t的值以及函数![]() 在区间[
在区间[![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题错误的是( )
A.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
B.设![]() ,且
,且![]() ,则
,则![]()
C.在残差图中,残差点分布的带状区域的宽带越狭窄,其模型拟合的精度越高
D.已知变量x和y满足关系![]() ,变量y与z正相关,则x与z负相关
,变量y与z正相关,则x与z负相关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导数![]() 满足f(x)+x
满足f(x)+x![]() >
>![]() 对x∈R恒成立,且实数x,y满足xf(x)﹣yf(y)>f(y)﹣f(x),则下列关系式恒成立的是( )
对x∈R恒成立,且实数x,y满足xf(x)﹣yf(y)>f(y)﹣f(x),则下列关系式恒成立的是( )
A.![]() B.ln(x2+1)>ln(y2+1)
B.ln(x2+1)>ln(y2+1)
C.![]() D.x﹣y>sinx﹣siny
D.x﹣y>sinx﹣siny
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x+c,若不等式f(x)<0的解集是{x|-4<x<2}.
(1)求f(x)的解析式;
(2)判断f(x)在(0,+∞)上的单调性,并用定义证明;
(3)若函数f(x)在区间[m,m+2]上的最小值为-5,求实数m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com