定义F(x,y)=(1+x)y,x,y∈(0,+∞)
(1)令函数f(x)=F(1,log2(x2-4x+9))的图象为曲线c1,曲线c1与y轴交于点A(0,m),过坐标原点O作曲线c1的切线,切点为B(n,t)(n>0)设曲线c1在点A、B之间的曲线段与OA、OB所围成图形的面积为S,求S的值;
(2)当x,y∈N*且x<y时,证明F(x,y)>F(y,x).
【答案】
分析:(1)求出f(x)的解析式,求出A的坐标,利用曲线在切点处的导数值是曲线的切线斜率,切点在曲线上,列出方程组求出B的坐标,将曲边图象的面积用定积分表示,利用微积分基本定理求出面积.
(2)构造函数h(x),求出其导函数判断导函数的符号,判断出h(x)的单调性,利用其单调性得到不等式,利用不等式的性质得证.
解答:解:(1)∵F(x,y)=(1+x)
y∴f(x)=F(1,log
2(x
2-4x+9))=2
log2(x
2-4x+9)=x
2-4x+9
故A(0,9)
f'(x)=2x-4,过O作C
1的切线,切点为B(n,t)(n>0),
∴
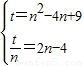
解得B(3,6)
∴
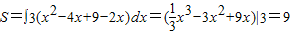
(2)令
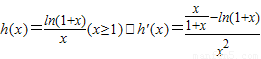
令
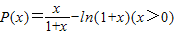
∴
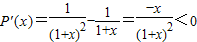
∴P(x)在[0,+∞)单调递减.
∴当x>0时,有P(x)<P(0),
∴当x≥1时有h'(x)<0∴h(x)在[1,+∞)上单调递减.
∴1≤x<y时,有
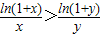
yln(1+x)>xln(1+y)
∴(1+x)
y>(1+y)
x∴当x,y∈N
*且x<y时,F(x,y)>F(y,x)
点评:本题考查导数的几何意义|导数在曲线切点处的值是曲线的切线斜率、利用定积分求曲边梯形的面积、
利用导数研究函数的单调性、不等式的性质.

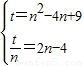 解得B(3,6)
解得B(3,6)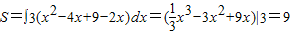
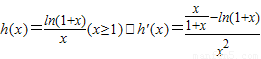
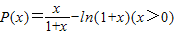 ∴
∴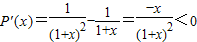
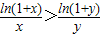


 发散思维新课堂系列答案
发散思维新课堂系列答案