
【题目】如图,正方形ABCD的边长为1,P,Q分别为AB,DA上动点,且△APQ的周长为2,设 AP=x,AQ=y. 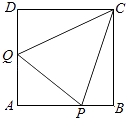
(1)求x,y之间的函数关系式y=f(x);
(2)判断∠PCQ的大小是否为定值?并说明理由;
(3)设△PCQ的面积分别为S,求S的最小值.
【答案】
(1)解:由已知可得PQ=2﹣x﹣y,根据勾股定理有(2﹣x﹣y)2=x2+y2,
化简得:y= ![]() (0<x<1)
(0<x<1)
(2)解:tan∠DCQ=1﹣y,tan∠BCP=1﹣x,
tan(∠DCQ+∠BCP)= ![]() =1
=1
∵∠DCQ+∠BCP∈(0, ![]() ),
),
∴∠DCQ+∠BCP= ![]() ,
,
∴∠PCQ= ![]() ﹣(∠DCQ+∠BCP)=
﹣(∠DCQ+∠BCP)= ![]() ,(定值)
,(定值)
(3)解:S=1﹣ ![]() ﹣
﹣ ![]() (1﹣x)﹣
(1﹣x)﹣ ![]() (1﹣y)=
(1﹣y)= ![]() (x+y﹣xy)=
(x+y﹣xy)= ![]()
![]()
令t=2﹣x,t∈(1,2),
∴S= ![]() (t+
(t+ ![]() )﹣1,
)﹣1,
∴t= ![]() 时,S的最小值为
时,S的最小值为 ![]() ﹣1
﹣1
【解析】(1)由已知可得PQ=2﹣x﹣y,根据勾股定理有(2﹣x﹣y)2=x2+y2 , 即可求x,y之间的函数关系式y=f(x);(2)求得∴∠DCQ+∠BCP= ![]() ,即可判断∠PCQ的大小;(3)表示△PCQ的面积,利用基本不等式求S的最小值.
,即可判断∠PCQ的大小;(3)表示△PCQ的面积,利用基本不等式求S的最小值.


科目:高中数学 来源: 题型:
【题目】设f(n)=(1+ ![]() )n﹣n,其中n为正整数.
)n﹣n,其中n为正整数.
(1)求f(1),f(2),f(3)的值;
(2)猜想满足不等式f(n)<0的正整数n的范围,并用数学归纳法证明你的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2 , x1+x2=1﹣a,则( )
A.f(x1)<f(x2)
B.f(x1)=f(x2)
C.f(x1)>f(x2)
D.f(x1)与f(x2)的大小不能确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在[﹣1,1]上的奇函数,当x∈[﹣1,0]时,函数解析式为 ![]() .
.
(Ⅰ)求f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC的四个顶点都在球D的表面上,PA⊥平面ABC,AB⊥BC,PA=3,AB=BC=2,则球O的表面积为( )
A.13π
B.17π
C.52π
D.68π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在海岸线![]() 一侧
一侧![]() 处有一个美丽的小岛,某旅游公司为方便游客,在
处有一个美丽的小岛,某旅游公司为方便游客,在![]() 上设立了
上设立了![]() 两个报名点,满足
两个报名点,满足![]() 中任意两点间的距离为
中任意两点间的距离为![]() .公司拟按以下思路运作:先将
.公司拟按以下思路运作:先将![]() 两处游客分别乘车集中到
两处游客分别乘车集中到![]() 之间的中转点
之间的中转点![]() 处(点
处(点![]() 异于
异于![]() 两点),然后乘同一艘轮游轮前往
两点),然后乘同一艘轮游轮前往![]() 岛.据统计,每批游客
岛.据统计,每批游客![]() 处需发车2辆,
处需发车2辆, ![]() 处需发车4辆,每辆汽车每千米耗费
处需发车4辆,每辆汽车每千米耗费![]() 元,游轮每千米耗费
元,游轮每千米耗费![]() 元.(其中
元.(其中![]() 是正常数)设∠
是正常数)设∠![]() ,每批游客从各自报名点到
,每批游客从各自报名点到![]() 岛所需运输成本为
岛所需运输成本为![]() 元.
元.
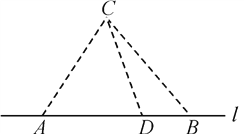
(1) 写出![]() 关于
关于![]() 的函数表达式,并指出
的函数表达式,并指出![]() 的取值范围;
的取值范围;
(2) 问:中转点![]() 距离
距离![]() 处多远时,
处多远时, ![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() sin(x+
sin(x+ ![]() )cos(x+
)cos(x+ ![]() )+sin2x+a的最大值为1.
)+sin2x+a的最大值为1.
(1)求函数f(x)的单调递增区间;
(2)将f(x)的图象向左平移 ![]() 个单位,得到函数g(x)的图象,若方程g(x)=m在x∈[0,
个单位,得到函数g(x)的图象,若方程g(x)=m在x∈[0, ![]() ]上有解,求实数m的取值范围.
]上有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四边形ABCD中,已知 ![]() ∥
∥ ![]() ,
, ![]() =(6,1),
=(6,1), ![]() =(x,y),
=(x,y), ![]() =(﹣2,﹣3).
=(﹣2,﹣3).
(1)求用x表示y的关系式;
(2)若 ![]() ⊥
⊥ ![]() ,求x、y值.
,求x、y值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com