
【题目】设函数 ![]() .
.
(Ⅰ)当 ![]() 时,讨论
时,讨论 ![]() 的单调性;
的单调性;
(Ⅱ)设 ![]() ,若
,若 ![]() 恒成立,求
恒成立,求 ![]() 的取值范围
的取值范围
【答案】解:(Ⅰ)由已知,当 ![]() 时,
时, ![]() ,
,
∴ ![]() ,
,
∵ ![]() 在
在 ![]() 上单调递增,且
上单调递增,且 ![]() ,
,
∴ ![]() 时,
时, ![]() 时,
时, ![]() ,
,
∴ ![]() 在
在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增.
上单调递增.
(Ⅱ)(方法一)由题可得, ![]() ,
,
则 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() 在
在 ![]() 上单调递增,
上单调递增, ![]() ,
, 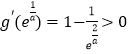 ,
,
∴ ![]() 使得
使得 ![]() ,则
,则 ![]() ,
,
由 ![]() 知
知 ![]() ,且
,且 ![]() 时,
时, ![]() 时,
时, ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,
,
∴ ![]() 的取值范围是
的取值范围是 ![]() .
.
(方法二)由题可得 ![]() 恒成立,
恒成立,
令 ![]() ,则
,则 ![]() ,
,
∴ ![]() 时,
时, ![]() 时,
时, ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,解得:
,解得: ![]() ,
,
∴ ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)法一:求出g(x)的导数,得到g(x)的最小值,从而求出a的范围即可;法二:问题转化为![]() 恒成立,令
恒成立,令![]() ,根据函数的单调性求出a的范围即可.
,根据函数的单调性求出a的范围即可.
【考点精析】解答此题的关键在于理解函数的单调性的相关知识,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某购物网站在2017年11月开展“全部6折”促销活动,在11日当天购物还可以再享受“每张订单金额(6折后〕满300元时可减免100元”.小淘在11日当天欲购入原价48元(单价)的商品共42件,为使花钱总数最少,他最少需要下的订单张数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且 ![]()

(1)求证:不论 ![]() 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD ?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.函数 ![]() 的图象与直线
的图象与直线 ![]() 可能有两个交点;
可能有两个交点;
B.函数 ![]() 与函数
与函数 ![]() 是同一函数;
是同一函数;
C.对于 ![]() 上的函数
上的函数 ![]() ,若有
,若有 ![]() ,那么函数
,那么函数 ![]() 在
在 ![]() 内有零点;
内有零点;
D.对于指数函数 ![]() (
( ![]() )与幂函数
)与幂函数 ![]() (
( ![]() ),总存在一个
),总存在一个 ![]() ,当
,当 ![]() 时,就会有
时,就会有 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如下图,汉诺塔问题是指有3根杆子A,B,C.B杆上有若干碟子,把所有碟子从B杆移到A杆上,每次只能移动一个碟子,大的碟子不能叠在小的碟子上面.把B杆上的4个碟子全部移到A杆上,最少需要移动( )次. ( )



A.12 B.15 C.17 D.19
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量 ![]() 与
与 ![]() 的随机变量
的随机变量 ![]() 越大,说明“
越大,说明“ ![]() 与
与 ![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型 ![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设 ![]() ,将其变换后得到线性方程
,将其变换后得到线性方程 ![]() ,则
,则 ![]() 的值分别是
的值分别是 ![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为 ![]() 中,
中, ![]() ,则
,则 ![]() .
.
④如果两个变量 ![]() 与
与 ![]() 之间不存在着线性关系,那么根据它们的一组数据
之间不存在着线性关系,那么根据它们的一组数据 ![]() 不能写出一个线性方程
不能写出一个线性方程
正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com