Question

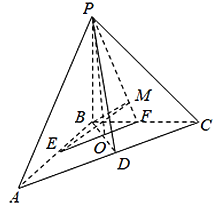
【题目】如图：在三棱锥中，面，是直角三角形，，，，点、、分别为、、的中点.

（1）求证：；

（2）求直线与平面所成的角的正弦值；

（3）求二面角的正切值.

Answer 1

【答案】（1）证明见解析；（2）；（3）.

【解析】

（1）连接，证明出平面，即可证得；

（2）连接交于点，由（1）知平面，可得直线与平面所成的角为，通过解，可计算出，进而得出结果；

（3）过点作于点，连接，证明出平面，可得出二面角的平面角为，然后解，即可计算出，进而得出结果.

（1）连接，在中，.

，点为的中点，.

又平面，平面，，

，平面，

、分别为、的中点，，平面，

平面，；

（2）连接交于点，由（1）知平面，

为直线与平面所成的角，且平面，.

平面，、平面，，，

又，，

，，

在中，，

因此，直线与平面所成的角的正弦值为；

（3）过点作于点，连接，

，，,平面，即平面，

平面，，

又，，平面，

平面，，

所以，为二面角的平面角.

在中，，所以，.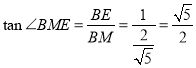

因此，二面角的正切值为.