
【题目】已知在△ABC中,∠A,∠B,∠C的对边分别为a,b,c,且a2=b(b+c).
(1)求证:∠A=2∠B;
(2)若a= ![]() b,判断△ABC的形状.
b,判断△ABC的形状.
【答案】
(1)证明:a2=b(b+c),
即BC2=AC(AC+AB),
延长CA至D,使AD=AB,连接DB.
则∠BAC=2∠D.
∴BC2=ACCD, ![]() ,
,
又∠C=∠C,
∴△BCA∽△DCB,故∠D=∠ABC.
∴∠BAC=2∠ABC
(2)解:∵a= ![]() b,
b,
∴a2=3b2,
又a2=b(b+c),
∴3b2=b2+bc,c=2b.
∴a2+b2=4b2,
c2=(2b)2=4b2.
即a2+b2=c2.
△ABC为直角三角形
【解析】(1)延长CA至D,使AD=AB,连接DB.根据a2=b(b+c)得到△BCA∽△DCB,然后由三角形中角的关系得答案;(2)由a= ![]() b结合a2=b(b+c)得到a2+b2=c2 , 说明△ABC为直角三角形.
b结合a2=b(b+c)得到a2+b2=c2 , 说明△ABC为直角三角形.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】海中一小岛![]() 的周围
的周围![]()
![]() 内有暗礁,海轮由西向东航行至
内有暗礁,海轮由西向东航行至![]() 处测得小岛
处测得小岛![]() 位于北偏东
位于北偏东![]() ,航行8
,航行8![]() 后,于
后,于![]() 处测得小岛
处测得小岛![]() 在北偏东
在北偏东![]() (如图所示).
(如图所示).

(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘海轮在![]() 处改变航向为东偏南
处改变航向为东偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+xlnx(a∈R)
(1)若函数f(x)在区间[e,+∞)上为增函数,求a的取值范围;
(2)当a=1且k∈Z时,不等式k(x﹣1)<f(x)在x∈(1,+∞)上恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cosα﹣
=(cosα﹣ ![]() ,﹣1),
,﹣1), ![]() =(sinα,1),
=(sinα,1), ![]() 与
与 ![]() 为共线向量,且α∈[﹣
为共线向量,且α∈[﹣ ![]() ,0].
,0].
(1)求sinα+cosα的值;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数)
为参数)
以![]() 为极点,
为极点, ![]() 轴为正半轴为极轴建立极坐标系,曲线
轴为正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点。
两点。
(Ⅰ)若![]() ,求
,求![]() ;
;
(Ⅱ)若点![]() 是曲线
是曲线![]() 上不同于
上不同于![]() ,
, ![]() 的动点,求
的动点,求![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 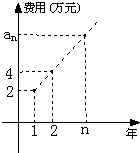
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过定点P(2,0)的直线l与曲线y= ![]() 相交于A,B两点,O为坐标原点,当△AOB的面积取最大时,直线的倾斜角可以是:①30°;②45°;③60°;④120°⑤150°.其中正确答案的序号是 . (写出所有正确答案的序号)
相交于A,B两点,O为坐标原点,当△AOB的面积取最大时,直线的倾斜角可以是:①30°;②45°;③60°;④120°⑤150°.其中正确答案的序号是 . (写出所有正确答案的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com