
分析 作出椭圆,然后分别过A,B作左准线、右准线的垂线为AC,BD,再分别过点F′,B作AC,x轴的垂线为F′E′,BE,可设BF=h,这样根据椭圆的第二定义及已知条件,便可建立关于h的方程,解出h,这时便可得出椭圆的离心率.
解答  解:如图,分别过A,B作左准线的垂线AC,垂足为C,右准线的垂线BD,垂足为D,作F′E′⊥AC,垂足为E′,过B作x轴的垂线,垂足为E,设BF=h,则AF′=2h;
解:如图,分别过A,B作左准线的垂线AC,垂足为C,右准线的垂线BD,垂足为D,作F′E′⊥AC,垂足为E′,过B作x轴的垂线,垂足为E,设BF=h,则AF′=2h;
又∠AF′E′=∠FBE=30°;
∴$AE′=h,FE=\frac{1}{2}h$;
∴$AC=\frac{{a}^{2}}{c}-c+h,BD=\frac{{a}^{2}}{c}-c-\frac{1}{2}h$;
∴根据椭圆的第二定义,$\frac{AF′}{AC}=\frac{BF}{BD}=e$,e为椭圆离心率;
即$\frac{2h}{\frac{{a}^{2}}{c}-c+h}=\frac{h}{\frac{{a}^{2}}{c}-c-\frac{1}{2}h}$;
∴$h=\frac{1}{2}(\frac{{a}^{2}}{c}-c)$;
∴$e=\frac{\frac{1}{2}(\frac{{a}^{2}}{c}-c)}{\frac{{a}^{2}}{c}-c-\frac{1}{4}(\frac{{a}^{2}}{c}-c)}=\frac{2}{3}$;
即椭圆的离心率为$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 考查椭圆的标准方程,椭圆的焦点,椭圆的准线方程,以及椭圆的第二定义,根据椭圆的第二定义求椭圆的离心率.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{7}$ | C. | 3 | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [0,1] | C. | [1,+∞) | D. | [-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>a>c | B. | a>c>b | C. | c>a>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
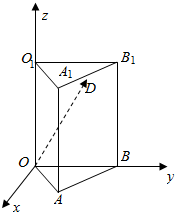 如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,
如图,在底面是边长为4的等边三角形的直三棱柱ABO-A1B1O1中,|AA1|=6,D为A1B1的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com