
【题目】已知函数![]() .
.
(![]() )若
)若![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值.
的值.
(![]() )求函数
)求函数![]() 的单调区间.
的单调区间.
(![]() )若
)若![]() 在
在![]() 上没有零点,求实数
上没有零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)单调增区间为
;(2)单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)求导,根据题意得![]() ,解得
,解得![]() ,再检验即可;
,再检验即可;
(2)由![]() ,令
,令![]() ,得增区间,令
,得增区间,令![]() 得减区间;
得减区间;
(3)要使![]() 在
在![]() 上没有零点,只需在
上没有零点,只需在![]() 上
上![]() 或
或![]() ,又
,又![]() ,只需在区间
,只需在区间![]() 上,
上,![]() ,进而转为研究函数最小值即可.
,进而转为研究函数最小值即可.
试题解析:
(![]() )
)![]() 的定义域为
的定义域为![]() ,且
,且![]() .
.
∵![]() 在
在![]() 处取得极值,
处取得极值,
∴![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
当![]() 时,
时,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,
∴函数![]() 在
在![]() 处取得极小值,
处取得极小值,
故![]() .
.
(![]() )
)![]() .
.
令![]() ,解得
,解得![]() ;
;
令![]() ,解得
,解得![]() ,
,
∴函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(![]() )要使
)要使![]() 在
在![]() 上没有零点,只需在
上没有零点,只需在![]() 上
上![]() 或
或![]() ,
,
又![]() ,只需在区间
,只需在区间![]() 上,
上,![]() .
.
①当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,则
上单调递减,则![]() ,
,
解得![]() 与
与![]() 矛盾.
矛盾.
②当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
![]() ,
,
解得![]() ,
,
∴![]() .
.
③当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() ,满足题意,
,满足题意,
综上所述,实数![]() 的取值范围是:
的取值范围是:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,已知点A(-2,0),直角顶点B(0,-2![]() ),点C在x轴上。
),点C在x轴上。
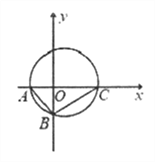
(1)求Rt△ABC外接圆的方程;
(2)求过点(-4,0)且与Rt△ABC外接圆相切的直线的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4﹣1:平面几何
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
(1)求证:∠DEA=∠DFA;
(2)若∠EBA=30°,EF= ![]() ,EA=2AC,求AF的长.
,EA=2AC,求AF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|2x﹣a|﹣1.
①当a=0时,不等式f(x)+1>0的解集为_____;
②若函数f(x)有三个不同的零点,则实数a的取值范围是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com