
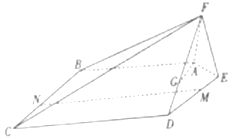
 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.分析 (1)点G为靠近D的三等分点,在线段CD取一点H,使得CH=2,连结AH,GH,即可得到AH∥BC,由点G为靠近D的三等分点,进一步求得GH∥CF,即可得结论;
(2)连接BD,求得AE,BD,又AB=DE,求出∠AED,取AE的中点K,连接FK,得到FK⊥KM,设ME=x(0<x<2),求出KM,又DM=FM=KM2+FK2,即可求出x的值,则三棱锥A-BMF的体积可求.
解答 解:(1)点G为靠近D的三等分点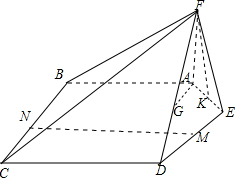
在线段CD取一点H,使得CH=2,连结AH,GH,
∵∠ABC=∠BCD=90°,
∴AB∥CD.
又AB=CH,∴四边形ABCH为平行四边形,∴AH∥BC.
∵点G为靠近D的三等分点,
∴FG:GD=CH:HD=2:1,∴GH∥CF.
∵AH∩GH=H,∴平面AGH∥平面BCF,而AG?平面AGH,∴AG∥平面BCF;
(2)连接BD,根据条件求得$AE=\sqrt{2}$,$BD=3\sqrt{2}$,又AB=DE=2,∴∠AED=135°.
取AE的中点K,连接FK,∵AF=EF,∴FK⊥AE,又平面AEF⊥平面ABCDE,∴FK⊥平面ABCDE,∴FK⊥KM.
设ME=x(0<x<2),∵$KE=\frac{\sqrt{2}}{2}$,∴KM=$(\frac{\sqrt{2}}{2})^{2}+{x}^{2}-2x×\frac{\sqrt{2}}{2}cos135°$=${x}^{2}+x+\frac{1}{2}$.
∵翻折后,D与F重合,∴DM=FM.
∴DM=FM=KM2+FK2,∴(2-x)2-x2+x+1⇒x=$\frac{3}{5}$.
∴VA-BMF=VF-ABM=$\frac{1}{3}×FK×\frac{1}{2}×AB×(ME+1)$=$\frac{1}{6}×\frac{\sqrt{2}}{2}×2×\frac{8}{5}=\frac{4\sqrt{2}}{15}$.
点评 本题考查空间几何体的体积,直线与平面的位置关系,平面与平面的位置关系的判断与证明,考查空间想象能力以及逻辑推理计算能力,是中档题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\sqrt{x^2},g(x)=x$ | B. | $f(x)=\frac{{{x^2}-1}}{x-1},g(x)=x+1$ | ||
| C. | $f(x)=\sqrt{{x^2}-4},g(x)=\sqrt{x+2}\sqrt{x-2}$ | D. | $f(x)=lg2-lgx,g(x)=lg\frac{2}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $20(\sqrt{3}+\sqrt{6})$海里/时 | B. | $20(\sqrt{6}-\sqrt{3})$海里/时 | C. | $20(\sqrt{2}+\sqrt{6})$海里/时 | D. | $20(\sqrt{6}-\sqrt{2})$海里/时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com