
【题目】设直线l的方程为y=kx+b(其中k的值与b无关),圆M的方程为x2+y2﹣2x﹣4=0.
(1)如果不论k取何值,直线l与圆M总有两个不同的交点,求b的取值范围;
(2)b=1,l与圆交于A,B两点,求|AB|的最大值和最小值.
【答案】
(1)解:若不论k取何值,直线l与圆M总有两个不同的交点,
则(0,b)点在圆M:x2+y2﹣2x﹣4=0的内部,
即b2﹣4<0,
解得:﹣2<b<2
(2)解:当b=1时,l必过(0,1)点,
当l过圆心时,|AB|取最大值,即圆的直径,
由M:x2+y2﹣2x﹣4=0的半径r= ![]() ,
,
故|AB|的最大值为2 ![]() ,
,
当l和过(0,1)的直径垂直时,|AB|取最小值.
此时圆心M(1,0)到(0,1)的距离d= ![]() ,
,
|AB|=2 ![]() =2
=2 ![]() ,
,
故|AB|的最小值为2 ![]()
【解析】(1)若不论k取何值,直线l与圆M总有两个不同的交点,则(0,b)点在圆M:x2+y2﹣2x﹣4=0的内部,进而得到b的取值范围;(2)b=1时,l必过(0,1)点,当l过圆心时,|AB|取最大值,当l和过(0,1)的直径垂直时,|AB|取最小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形.
(Ⅰ)求二面角P﹣AB﹣C的大小;
(Ⅱ)在线段AB上是否存在一点E,使平面PCE⊥平面PCD?若存在,请指出点E的位置并证明,若不存在请说明理由.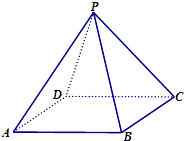
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2alnx.
(1)若函数f(x)的图象在(2,f(2))处的切线斜率为1,求实数a的值;
(2)求函数f(x)的单调区间;
(3)若函数 ![]() 在[1,2]上是减函数,求实数a的取值范围.
在[1,2]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下: 
(1)求该运动员得分的中位数和平均数;
(2)估计该运动员每场得分超过10分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com