
分析 (1)由已知求出cos2α,再由降幂公式求得sinα和cosα的值;
(2)由已知利用配角思想求出sin2β、cos2β的值,得到tan2β,再由(1)求出tanα,代入两角和的正切得答案.
解答 解:(1)∵α∈(0,$\frac{π}{4}$),∴2α∈(0,$\frac{π}{2}$),
又sin2α=$\frac{4}{5}$,∴cos2α=$\sqrt{1-si{n}^{2}2α}=\sqrt{1-(\frac{4}{5})^{2}}=\frac{3}{5}$,
由cos2α=1-2sin2α,得
$sinα=\sqrt{\frac{1-cos2α}{2}}=\sqrt{\frac{1-\frac{3}{5}}{2}}=\frac{\sqrt{5}}{5}$,
∴cosα=$\sqrt{1-si{n}^{2}α}=\sqrt{1-(\frac{\sqrt{5}}{5})^{2}}=\frac{2\sqrt{5}}{5}$;
(2)由β∈($\frac{π}{4}$,$\frac{π}{2}$),得$β-\frac{π}{4}$∈(0,$\frac{π}{4}$),
又sin(β-$\frac{π}{4}$)=$\frac{3}{5}$,∴cos(β-$\frac{π}{4}$)=$\frac{4}{5}$,
∴sinβ=sin[($β-\frac{π}{4}$)+$\frac{π}{4}$]=sin($β-\frac{π}{4}$)cos$\frac{π}{4}$+cos($β-\frac{π}{4}$)sin$\frac{π}{4}$
=($\frac{3}{5}+\frac{4}{5}$)×$\frac{\sqrt{2}}{2}$=$\frac{7\sqrt{2}}{10}$.
则cosβ=$\sqrt{1-si{n}^{2}β}=\sqrt{1-(\frac{7\sqrt{2}}{10})^{2}}=\frac{\sqrt{2}}{10}$.
∴sin2β=2sinβcosβ=2×$\frac{7\sqrt{2}}{10}×\frac{\sqrt{2}}{10}$=$\frac{7}{25}$.
则cos2β=$-\frac{24}{25}$,
∴tan2$β=-\frac{7}{24}$.
由(1)知,tan$α=\frac{1}{2}$,
∴tan(α+2β)=$\frac{tanα+tan2β}{1-tanαtan2β}$=$\frac{\frac{1}{2}-\frac{7}{24}}{1+\frac{1}{2}×\frac{7}{24}}$=$\frac{2}{11}$.
点评 本题考查两角和与差的三角函数,考查倍角公式、同角三角函数的基本关系式等的应用,属中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$i | C. | -$\frac{2\sqrt{5}}{5}$ | D. | -$\frac{2\sqrt{5}}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
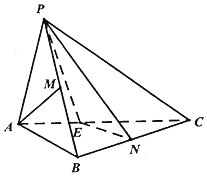 如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.
如图,三棱锥P-ABC中,BC⊥平面PAB,PA=PB=AB=6,BC=9,点M,N分别为PB,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R,${x_0}^2-2{x_0}+1≥0$ | B. | 存在x0∈R,${x_0}^2-2{x_0}+1≤0$ | ||
| C. | 存在x0∈R,${x_0}^2-2{x_0}+1<0$ | D. | 对任意的x∈R,x2-2x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com