
分析 本题考查的知识点是古典概型的意义,关键是要找出连续抛掷两次骰子分别得到的点数m,n作为点P的坐标所得P点的总个数,及点P(m,n)落在以坐标原点为圆心,4为半径的圆内的个数,代入古典概型计算公式即可求解.
解答 解:连续抛掷两次骰子分别得到的点数m,n作为点P的坐标所得P点有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6).共36个
其中点P(m,n)落在以坐标原点为圆心,4为半径的圆内的有:(1,1)(1,2)(1,3)(2,1)(2,2)(2,3)(3,1)(3,2)共8个
故点P(m,n)落在以坐标原点为圆心,4为半径的圆内的概率P=$\frac{2}{9}$,
故答案为$\frac{2}{9}$.
点评 古典概型要求所有结果出现的可能性都相等,强调所有结果中每一结果出现的概率都相同.弄清一次试验的意义以及每个基本事件的含义是解决问题的前提,正确把握各个事件的相互关系是解决问题的关键.解决问题的步骤是:计算满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式进行求解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
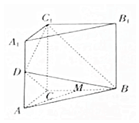 如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.
如图,在直三棱柱ABC-A1B1C1中,D,M分别是AA1,BC的中点,∠CDC1=90°,在△ABC中,AB=2AC,∠BAC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a<b,则a-1<b-1 | B. | 若a-1>b-1,则a>b | C. | 若a≤b,则a-1≤b-1 | D. | 若a-1≤b-1,则a≤b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | $\frac{1}{8}$ | C. | 3 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com