
【题目】已知函数f(x)=x2(ex+e﹣x)﹣(2x+1)2(e2x+1+e﹣2x﹣1),则满足f(x)>0的实数x的取值范围为( )
A.(﹣1,﹣ ![]() )
)
B.(﹣∞,﹣1)
C.(﹣ ![]() ,+∞)
,+∞)
D.(﹣∞,﹣1)∪(﹣ ![]() ,+∞)
,+∞)
【答案】A
【解析】解:设g(x)=x2(ex+e﹣x),则由f(x)>0,得g(x)>g(2x+1),
∵g(﹣x)=g(x),∴g(x)为偶函数,
当x≥0时,g′(x)=2x(ex+e﹣x)+x2(ex﹣e﹣x)≥0,
∴函数g(x)在[0,+∞)上为增函数,
则由g(x)>g(2x+1),得|x|>|2x+1|,
解得:﹣1 ![]() .
.
故选:A.
【考点精析】本题主要考查了函数的值域的相关知识点,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() +
+ ![]() =1(a>b>0)的两个焦点为F1、F2 , 且椭圆E过点(0,
=1(a>b>0)的两个焦点为F1、F2 , 且椭圆E过点(0, ![]() ),(
),( ![]() ,﹣
,﹣ ![]() ),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△
),点A是椭圆上位于第一象限的一点,且△AF1F2的面积S△ ![]() =
= ![]() .
.
(1)求点A的坐标;
(2)过点B(3,0)的直线l与椭圆E相交于点P、Q,直线AP、AQ分别与x轴相交于点M、N,点C( ![]() ,0),证明:|CM||CN|为定值,并求出该定值.
,0),证明:|CM||CN|为定值,并求出该定值. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧棱垂直于底面,
中,侧棱垂直于底面, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:在棱![]() 上存在一点
上存在一点![]() ,使得平面
,使得平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤ω≤3,则居住满意度为二级;若0≤ω≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
人员编号 | 1 | 2 | 3 | 4 | 5 |
(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
人员编号 | 6 | 7 | 8 | 9 | 10 |
(x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(1)在这10名被调查者中任取两人,求这两人的居住满意度指标z相同的概率;
(2)从居住满意度为一级的被调查者中随机抽取一人,其综合指标为m,从居住满意度不是一级的被调查者中任取一人,其综合指标为n,记随机变量ξ=m﹣n,求随机变量ξ的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:如图,梯形ABCD中,AD∥BC,∠C= ![]() ,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF.
,以AB为直径的⊙O恰与CD相切于点E,⊙O交BC于F,连结EF. 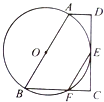
(1)求证:AD+BC=AB;
(2)求证:EF是AD与AB的等比中项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=bx﹣axlnx(a>0)的图象在点(1,f(1))处的切线与直线平y=(1﹣a)x行.
(1)若函数y=f(x)在[e,2e]上是减函数,求实数a的最小值;
(2)设g(x)= ![]() ,若存在x1∈[e,e2],使g(x1)≤
,若存在x1∈[e,e2],使g(x1)≤ ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com