
 }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)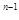 +2 (n为正整数).
+2 (n为正整数). =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项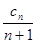 =
=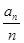 ,T
,T = c
= c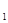 +c
+c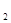 +···+c
+···+c ,求T
,求T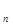 .
. =
=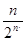 . ⑵T
. ⑵T =3—
=3—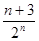 .
.  }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)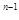 +2 (n为正整数).
+2 (n为正整数). =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项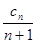 =
=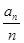 ,然后运用错位相减法得到数列的和式。
,然后运用错位相减法得到数列的和式。 = —an—(
= —an—( )
)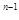 +2,得S
+2,得S = —a
= —a —(
—( )
) +2,两式相减,得a
+2,两式相减,得a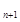 =
= + a
+ a +(
+( )
) ,即a
,即a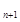 =
= a
a +(
+( )
)
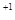 .---------------------------------------2分
.---------------------------------------2分 = —a
= —a —(
—( )
)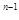 +2,令n=1,得a
+2,令n=1,得a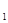 =
= .对于a
.对于a =
= a
a +(
+( )
)
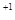 ,两端同时除以(
,两端同时除以( )
)
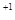 ,得2
,得2 a
a =2
=2 a
a +1,即数列{2
+1,即数列{2 a
a }是首项为2
}是首项为2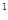 ·a
·a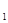 =1,公差为1的等差数列,故2
=1,公差为1的等差数列,故2 a
a =n,所以a
=n,所以a =
=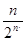 .------------------------------------6分
.------------------------------------6分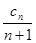 =
=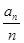 ,得c
,得c = (n+1)(
= (n+1)( )
) ,
, =2×
=2× +3×(
+3×( )
)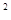 +4×(
+4×( )
)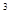 +···+(n+1) (
+···+(n+1) ( )
) ,①
,① T
T =2×(
=2×( )
)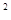 +3×(
+3×( )
)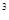 +4×(
+4×( )
)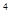 +···+(n+1) (
+···+(n+1) ( )
) ,②
,② T
T =1+(
=1+( )
)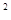 +(
+( )
)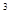 +···+(
+···+( )
) -(n+1) (
-(n+1) ( )
) =1+
=1+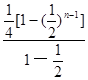 —
— )
) =
=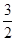 —
—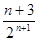 . 所以T
. 所以T =3—
=3—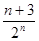 .------------------------------------12分
.------------------------------------12分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
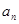 }是等差数列,且满足:a1+a2+a3=6,a5=5;
}是等差数列,且满足:a1+a2+a3=6,a5=5;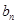 }满足:
}满足: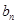 -
-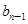 =
=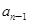 (n≥2,n∈N﹡),b1=1.
(n≥2,n∈N﹡),b1=1.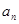 和
和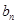 ;
;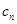 =
=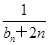 (n∈N﹡),若{
(n∈N﹡),若{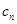 }的前n项和为
}的前n项和为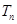 ,求
,求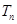 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com