[题目]已知椭圆和双曲线焦点F1 . F2相同.且离心率互为倒数.P是椭圆和双曲线在第一象限的交点.当∠F1PF2=60°时.椭圆的离心率为( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

【题目】已知椭圆和双曲线焦点F1 ， F2相同，且离心率互为倒数，P是椭圆和双曲线在第一象限的交点，当∠F1PF2=60°时，椭圆的离心率为（）
A.
B.
C.
D.

【答案】A
【解析】解：设F1P=m，F2P=n，F1F2=2c；
由余弦定理得，（2c）2=m2+n2﹣2mncos60°，即4c2=m2+n2﹣mn；
设a1是椭圆的长半轴，a2是双曲线的实半轴；
由椭圆及双曲线定义，得m+n=2a1 ， m﹣n=2a2；
∴m=a1+a2 ， n=a1﹣a2 ，将它们代入前式得3a22﹣4c2+a12=0；
∵离心率互为倒数；
∴ ，∴c2=a1a2；
∴ （a2﹣a1）=0；
根据题意，a2≠a1 ， ∴a1=3a2；
∴e1e2=
即3e12=1；
∴e1= ．
故选：A．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数，若存在x1 ， x2∈R，x1≠x2 ，使f（x1）=f（x2）成立，则实数a的取值范围是

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列四种说法：
①垂直于同一平面的所有向量一定共面；
②在△ABC中，已知，则∠A=60°；
③在△ABC中，sin2A=sin2B+sin2C+sinBsinC，则A=
④若a＞0，b＞0，a+b=2，则a2+b2≥2；
正确的序号有．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，DE∥BC，BC=2DE，CA⊥CB，CA⊥CD，CB⊥CD，F、G分别是AC、BC中点．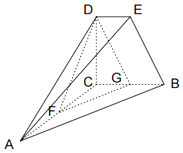
（1）求证：平面DFG∥平面ABE；
（2）若AC=2BC=2CD=4，求二面角E﹣AB﹣C的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在棱长为a的正方体ABCD﹣A1B1C1D1中，P为A1D1的中点，Q为A1B1上任意一点，E、F为CD上两点，且EF的长为定值，则下面四个值中不是定值的是（）
A.点P到平面QEF的距离
B.直线PQ与平面PEF所成的角
C.三棱锥P﹣QEF的体积
D.△QEF的面积

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，直角坐标系x′Oy所在的平面为β，直角坐标系xOy所在的平面为α，且二面角α﹣y轴﹣β的大小等于30°．已知β内的曲线C′的方程是3（x﹣2 ）2+4y2﹣36=0，则曲线C′在α内的射影在坐标系xOy下的曲线方程是．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图所示，点F1（﹣1，0），F2（1，0），动点M到点F2的距离是，线段MF1的中垂线交MF2于点P．

（1）当点M变化时，求动点P的轨迹G的方程；
（2）设直线l：y=kx+m与轨迹G交于M、N两点，直线F2M与F2N的倾斜角分别为α、β，且α+β=π，求证：直线l经过定点，并求该定点的坐标．