
【题目】已知点![]() 为圆
为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,点
,点![]() 为线段AB的中点,设点
为线段AB的中点,设点![]() 的轨迹为
的轨迹为![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)已知直线![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() ,若直线
,若直线![]() 的斜率之和为3,直线
的斜率之和为3,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
【答案】(1)![]() ;(2)恒过定点(
;(2)恒过定点(![]() ,
,![]() ).
).
【解析】
(1)设点![]() ,由题意可知
,由题意可知![]() ,得到
,得到![]() ,代入化简得到答案.
,代入化简得到答案.
(2)设M(x1,y1),B(x2,y2),考虑斜率存在和斜率不存在两种情况,联立方程,利用韦达定理,根据斜率和为3得到![]() ,得到定点.
,得到定点.
(1) 设点![]() ,由题意可知
,由题意可知![]() ,
,
![]() 为
为![]() 中点,即
中点,即![]() ,即
,即![]() ,
,
又点![]() 在圆上,
在圆上,![]() ,代入得
,代入得![]() ,得到轨迹方程为
,得到轨迹方程为![]() .
.
(2)设M(x1,y1),B(x2,y2),
①当l的斜率存在时,设l:y=kx+m,
由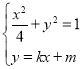 ,得
,得![]() ,
,
![]() ,即4k2﹣m2+1>0,
,即4k2﹣m2+1>0,
∴![]() ,
,![]() ,
,
∵直线QM,QN的斜率之和为3,∴![]() ,
,
∴2k+![]() =3,∴2k
=3,∴2k![]() =3,∴
=3,∴![]() ,
,![]() ,
,
当![]() 时,由 4k2﹣m2+1>0,故
时,由 4k2﹣m2+1>0,故![]() ,即
,即![]() 或
或![]() 时符合题意,
时符合题意,
此时直线l:y=kx+![]() 恒过定点(
恒过定点(![]() ,
,![]() );
);
②当l的斜率不存在时,x1=x2,y1=﹣y2,
∵直线QM,QN的斜率之和为3,∴![]() ,
,
∴x2=![]() ,此时直线l:x=
,此时直线l:x=![]() ,恒过定点(
,恒过定点(![]() ,
,![]() ).
).
综上所述:直线过定点(![]() ,
,![]() ).
).


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,![]() ,
,![]() ,M是以CD为直径的半圆周上的任意一点(与C,D均不重合),且平面
,M是以CD为直径的半圆周上的任意一点(与C,D均不重合),且平面![]() 平面ABCD.
平面ABCD.
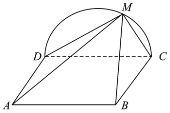
(1)求证:平面![]() 平面BCM;
平面BCM;
(2)当四棱锥![]() 的体积最大时,求AM与CD所成的角.
的体积最大时,求AM与CD所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】探月工程“嫦娥四号”探测器于2018年12月8日成功发射,实现了人类首次月球背面软着陆.以嫦娥四号为任务圆满成功为标志,我国探月工程四期和深空探测工程全面拉开序幕.根据部署,我国探月工程到2020年前将实现“绕、落、回”三步走目标.为了实现目标,各科研团队进行积极的备战工作.某科研团队现正准备攻克甲、乙、丙三项新技术,甲、乙、丙三项新技术独立被攻克的概率分别为![]() ,若甲、乙、丙三项新技术被攻克,分别可获得科研经费
,若甲、乙、丙三项新技术被攻克,分别可获得科研经费![]() 万,
万,![]() 万,
万,![]() 万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
万.若其中某项新技术未被攻克,则该项新技术没有对应的科研经费.
(1)求该科研团队获得![]() 万科研经费的概率;
万科研经费的概率;
(2)记该科研团队获得的科研经费为随机变量![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉三角是二项式系数在三角形中的一种排列,在欧洲这个表叫做帕斯卡三角形,帕斯卡是在1654年发现这一规律的,我国南宋数学家杨辉在1261年所著的《详解九章算法》一书中出现了如图所示的表,这是我国数学史上的一次伟大成就,如图所示,在“杨辉三角”中去除所有为1的项,依次构成数列,2,3,3,4,6,4,5 ,10 ,10,5,……,则此数列的前119项的和为__________.(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种工业机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:
方案一:交纳延保金700元,在延保的两年内可免费维修2次,超过2次每次收取维修费200元;
方案二:交纳延保金1000元,在延保的两年内可免费维修4次,超过4次每次收取维修费100元.
某工厂准备一次性购买2台这种机器.现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 20 | 10 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率.记X表示这2台机器超过质保期后延保的两年内共需维修的次数.
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,工厂选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量![]() (件)与单价
(件)与单价![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.

(1)根据周销售量图写出![]() (件)与单价
(件)与单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润![]() (元)与单价
(元)与单价![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn(n∈N*),等比数列{bn}的前n项和为Tn(n∈N*),已知a1=3,b1=1,a3+b2=10,S3﹣T2=11.
(Ⅰ)求数列{an}、{bn}的通项公式:
(Ⅱ)若数列{cn}满足c1=1,cn+1﹣cn=an,求c100;
(Ⅲ)设数列dn=anbn,求{dn}的前n项和Kn.
查看答案和解析>>
科目:高中数学 来源: 题型:
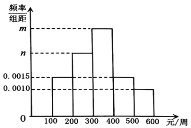
【题目】某网购平台为了解某市居民在该平台的消费情况,从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名,并绘制右图所示频率分布直方图,已知中间三组的人数可构成等差数列.
(1)求![]() 的值;
的值;
(2)分析人员对抽取对象每周的消费金额y与年龄x进一步分析,发现他们线性相关,得到回归方程![]() .已知100名使用者的平均年龄为38岁,试判断一名年龄为22岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
.已知100名使用者的平均年龄为38岁,试判断一名年龄为22岁的年轻人每周的平均消费金额为多少.(同一组数据用该区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种排卡游戏规则如下:将写有![]() 的九张卡片随机地排成一行,第一张卡片:左起)上的标数为
的九张卡片随机地排成一行,第一张卡片:左起)上的标数为![]() ,则将前
,则将前![]() 张卡片逆序排过来称为一次操作,无法操作时(即第一张卡片上的标数“1”)游戏停止.若一个排列无法操作,且恰由唯一的另一个排列经过一次操作得到,则此排列称为“二次终止排列”.在所有可能的排列中,求二次终止排列出现的概率.
张卡片逆序排过来称为一次操作,无法操作时(即第一张卡片上的标数“1”)游戏停止.若一个排列无法操作,且恰由唯一的另一个排列经过一次操作得到,则此排列称为“二次终止排列”.在所有可能的排列中,求二次终止排列出现的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com