
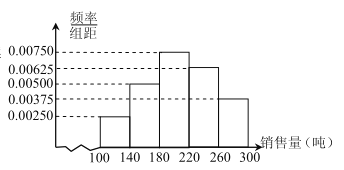
【题目】某企业为了增加某种产品的生产能力,提出甲、乙两个方案。甲方案是废除原有生产线并引进一条新生产线,需一次性投资1000万元,年生产能力为300吨;乙方案是改造原有生产线,需一次性投资700万元,年生产能力为200吨;根据市场调查与预测,该产品的年销售量的频率分布直方图如图所示,无论是引进新生产线还是改造原有生产线,设备的使用年限均为6年,该产品的销售利润为1.5万元/吨。
(Ⅰ)根据年销售量的频率分布直方图,估算年销量的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)将年销售量落入各组的频率视为概率,各组的年销售量用该组区间的中点值作年销量的估计值,并假设每年的销售量相互独立。
(i)根据频率分布直方图估计年销售利润不低于270万的概率;
(ii)以企业6年的净利润的期望值作为决策的依据,试判断该企业应选择哪个方案。(6年的净利润=6年销售利润-投资费用)
【答案】(Ⅰ)206(Ⅱ) (ⅰ)0.7(ⅱ)乙方案
【解析】
(Ⅰ)由频率分布直方图能求出年销量的平均数.
(Ⅱ)(i)该产品的销售利润为1.5万元/吨,由频率分布直方图得只有当年平均销量不低于180吨时年销售利润才不低于270万,由此能求出年销售利润不低于270万的概率.
(ii)分别求出甲方案6年的净利润的期望值和乙方案6年的净利润的期望值,由乙方案的净利润的期望值大于甲方案的净利润的期望值,得企业应该选择乙方案.
(Ⅰ)年销售量的平均数![]() (吨)
(吨)
(Ⅱ)(ⅰ)该产品的销售利润为![]() 万元/吨,由直方图可知只有当年平均销量不低于
万元/吨,由直方图可知只有当年平均销量不低于![]() 吨时,年销售利润才不低于
吨时,年销售利润才不低于![]() 万,
万,![]() 年销售利润不低于
年销售利润不低于![]() 万的概率
万的概率![]()
(ⅱ)设甲方案的年销售量为![]() 吨,由(Ⅰ)可知甲方案的年销售量的期望
吨,由(Ⅰ)可知甲方案的年销售量的期望![]() ,
,
所以甲方案6年的净利润的期望值为:![]() (万元)
(万元)
设乙方案的年销售量为![]() 吨,则乙方案的年销售量的分布列为:
吨,则乙方案的年销售量的分布列为:
|
|
|
|
|
|
|
|
![]() 乙方案的年销售量期望
乙方案的年销售量期望![]()
![]() 乙方案6年的净利润的期望值为:
乙方案6年的净利润的期望值为:![]() (万元)
(万元)
由上可知乙方案的净利润的期望值大于甲方案的净利润的期望值,故企业应选择乙方案。


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
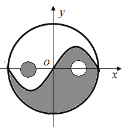
【题目】太极是中国古代的哲学术语,意为派生万物的本源.太极图是以黑白两个鱼形纹组成的圆形图案,俗称阴阳鱼.太极图形象化地表达了阴阳轮转,相反相成是万物生成变化根源的哲理.太极图形展现了一种互相转化,相对统一的形式美.按照太极图的构图方法,在平面直角坐标系中,圆![]() 被
被![]() 的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为
的图象分割为两个对称的鱼形图案,图中的两个一黑一白的小圆通常称为“鱼眼”,已知小圆的半径均为![]() ,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
,现在大圆内随机投放一点,则此点投放到“鱼眼”部分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是![]() (
(![]() ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是
≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是![]() .若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是
.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26 cm,则其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥S-ABC中,已知SC⊥平面ABC,AB=BC=CA![]() ,SC=2,D、E分别为AB、BC的中点.若点P在SE上移动,求△PCD面积的最小值.
,SC=2,D、E分别为AB、BC的中点.若点P在SE上移动,求△PCD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的两个焦点分别为F1(-1,0)、F2(1,0),短轴的两个端点分别为B1,B2
(1)若△F1B1B2为等边三角形,求椭圆C的方程;
(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com