
【题目】设函数![]() ,下述四个结论:
,下述四个结论:
①![]() 是偶函数;
是偶函数;
②![]() 的最小正周期为
的最小正周期为![]() ;
;
③![]() 的最小值为0;
的最小值为0;
④![]() 在
在![]() 上有3个零点
上有3个零点
其中所有正确结论的编号是( )
A.①②B.①②③C.①③④D.②③④
【答案】B
【解析】
根据函数相关知识对各选项逐个判断,即可得出其真假.
因为函数f(x)定义域为R,而且f(﹣x)=cos|2x|+|sinx|=f(x),所以f(x)是偶函数,①正确;
因为函数y=cos|2x|的最小正周期为π,y=|sinx|的最小正周期为π,所以f(x)的最小正周期为π,②正确;
f(x)=cos|2x|+|sinx|=cos2x+|sinx|=1﹣2sin2x+|sinx|=﹣2(|sinx|![]() )2
)2![]() ,而|sinx|∈[0,1],所以当|sinx|=1时,f(x)的最小值为0,③正确;
,而|sinx|∈[0,1],所以当|sinx|=1时,f(x)的最小值为0,③正确;
由上可知f(x)=0可得1﹣2sin2x+|sinx|=0,解得|sinx|=1或|sinx|![]() (舍去)
(舍去)
因此在[0,2π]上只有x![]() 或x
或x![]() ,所以④不正确.
,所以④不正确.
故选:B.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为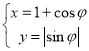 (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值与最小值.
的距离的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程,并求出曲线
的极坐标方程,并求出曲线![]() 与
与![]() 公共弦所在直线的极坐标方程;
公共弦所在直线的极坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() 点,且
点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点![]() ,
,![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的右下顶点,且
的右下顶点,且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 内,满足直线
内,满足直线![]() ,
,![]() 的斜率乘积为
的斜率乘积为![]() ,且直线
,且直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于点
于点![]() ,
,![]() .
.
①若![]() ,
,![]() 关于
关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
②若![]() 和
和![]() 的面积分别为
的面积分别为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司甲、乙两个班组分别试生产同一种规格的产品,已知此种产品的质量指标检测分数不小于70时,该产品为合格品,否则为次品,现随机抽取两个班组生产的此种产品各100件进行检测,其结果如下表:
质量指标检测分数 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
甲班组生产的产品件数 | 7 | 18 | 40 | 29 | 6 |
乙班组生产的产品件数 | 8 | 12 | 40 | 32 | 8 |
(1)根据表中数据,估计甲、乙两个班组生产该种产品各自的不合格率;
(2)根据以上数据,完成下面的2×2列联表,并判断是否有95%的把握认为该种产品的质量与生产产品的班组有关?
甲班组 | 乙班组 | 合计 | |
合格品 | |||
次品 | |||
合计 |
(3)若按合格与不合格比例,从甲班组生产的产品中抽取4件产品,从乙班组生产的产品中抽取5件产品,记事件A:从上面4件甲班组生产的产品中随机抽取2件,且都是合格品;事件B:从上面5件乙班组生产的产品中随机抽取2件,一件是合格品,一件是次品,试估计这两个事件哪一种情况发生的可能性大.
附:![]()
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com