【答案】
分析:(I)题目中欲证:“在R上有两个极值点”,利用导数的意义.即导函数有两个零点.从而转化为二次函数f′(x)=0的根的问题,利用根的判别式大于零解决即可.
(II)对函数 g(x)求导可得

由g'(x)=0,可得得x=a或-a,结合(I)中结论,从而可得a.
解答:证明:(I)因为f'(x)=x
2-2ax+(a
2-1)=[x-(a+1)][x-(a-1)],
令f'(x)=0,则x
1=a+1,x
2=a-1,------------------------------------------(2分)
则当x<a-1时,f'(x)>0,当a-1<x<a+1,f'(x)<0
所以x=a-1为f(x)的一个极大值点,-----------------------(4分)
同理可证x=a+1为f(x)的一个极小值点.-------------------------------------(5分)
另解:(I)因为f′(x)=x
2-2ax+(a
2-1)是一个二次函数,
且△=(-2a)
2-4(a
2-1)=4>0,-------------------------------------(2分)
所以导函数有两个不同的零点,
又因为导函数是一个二次函数,
所以函数f(x)有两个不同的极值点.---------------------------------------(5分)
(II) 因为
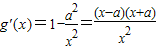
,
令g'(x)=0,则x
1=a,x
2=-a---------------------------------------(6分)
因为f(x)和g(x)有相同的极值点,且x
1=a和a+1,a-1不可能相等,
所以当-a=a+1时,
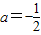
,当-a=a-1时,
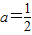
,
经检验,
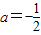
和
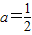
时,x
1=a,x
2=-a都是g(x)的极值点.--------------(8分)
点评:本题主要考查函数的导数、极值等基础知识,三次函数的单调性可借助于导函数(二次函数)来分析,解得本题不但要熟练掌握函数的导数的相关的知识,还要具备一定的逻辑推理的能力,此题对考生的能力要求较高.

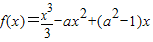 和
和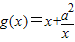
 由g'(x)=0,可得得x=a或-a,结合(I)中结论,从而可得a.
由g'(x)=0,可得得x=a或-a,结合(I)中结论,从而可得a.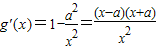 ,
,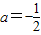 ,当-a=a-1时,
,当-a=a-1时,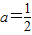 ,
,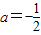 和
和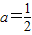 时,x1=a,x2=-a都是g(x)的极值点.--------------(8分)
时,x1=a,x2=-a都是g(x)的极值点.--------------(8分)

 和
和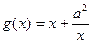
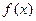 总有两个极值点;
总有两个极值点; 若
若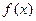 和
和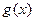 有相同的极值点,求
有相同的极值点,求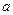 的值.
的值.