
°æƒø°øƒ≥∞ýÕ¨—ß¿˚”√π˙«ÏΩ⁄Ω¯––…Áª· µº˘£¨∂‘![]() À͵ƒ»À»∫Àʪ˙≥È»°
À͵ƒ»À»∫Àʪ˙≥È»°![]() »ÀΩ¯––¡À“ª¥Œ…˙ªÓœ∞πþ «∑Ò∑˚∫œµÕúπ€ƒÓµƒµ˜≤È£¨»Ù…˙ªÓœ∞πþ∑˚∫œµÕúπ€ƒÓµƒ≥∆Œ™°∞µÕú◊°±£¨∑Ò‘Ú≥∆Œ™°∞∑«µÕú◊°±£¨µ√µΩ»Áœ¬Õ≥º∆±Ì∫Õ∏˜ƒÍ¡‰∂Œ»À ˝∆µ¬ ∑÷≤º÷±∑ΩÕº£∫
»ÀΩ¯––¡À“ª¥Œ…˙ªÓœ∞πþ «∑Ò∑˚∫œµÕúπ€ƒÓµƒµ˜≤È£¨»Ù…˙ªÓœ∞πþ∑˚∫œµÕúπ€ƒÓµƒ≥∆Œ™°∞µÕú◊°±£¨∑Ò‘Ú≥∆Œ™°∞∑«µÕú◊°±£¨µ√µΩ»Áœ¬Õ≥º∆±Ì∫Õ∏˜ƒÍ¡‰∂Œ»À ˝∆µ¬ ∑÷≤º÷±∑ΩÕº£∫
◊È ˝ | ∑÷◊È | µÕú◊µƒ»À ˝ | ’º±æ◊ȵƒ∆µ¬ |
µ⁄“ª◊È |
| 120 | 0.6 |
µ⁄∂˛◊È |
| 195 |
|
µ⁄»˝◊È |
| 100 | 0.5 |
µ⁄Àƒ◊È |
|
| 0.4 |
µ⁄ŒÂ◊È |
| 30 | 0.3 |
µ⁄¡˘◊È |
| 15 | 0.3 |
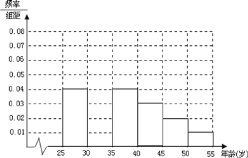
£®1£©≤π»´∆µ¬ ∑÷≤º÷±∑ΩÕº≤¢«Û![]() °¢
°¢![]() °¢
°¢![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©¥”![]() À̓͡‰∂Œµƒ°∞µÕú◊°±÷–≤…”√∑÷≤„≥È—˘∑®≥È»°18»À≤Œº”ªßÕ‚µÕú×ȪÓ∂Ø£¨»Á∫Œ≥È»°£ø
À̓͡‰∂Œµƒ°∞µÕú◊°±÷–≤…”√∑÷≤„≥È—˘∑®≥È»°18»À≤Œº”ªßÕ‚µÕú×ȪÓ∂Ø£¨»Á∫Œ≥È»°£ø
°æ¥∞∏°ø£®1£©ÕºœÒº˚Ω‚Œˆ£¨ ![]() £®2£©¿˚”√≥È«©∑®ªÚÀʪ˙ ˝±Ì∑®‘⁄
£®2£©¿˚”√≥È«©∑®ªÚÀʪ˙ ˝±Ì∑®‘⁄![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°12»À£¨¥”
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°12»À£¨¥”![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°6»À.
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°6»À.
°æΩ‚Œˆ°ø
£®1£©”…∆µ¬ ∑÷≤º÷±∑ΩÕº÷–À˘”–∆µ¬ (√ʪ˝)∫ÕŒ™1ø…µ√![]() µƒ∆µ¬ £¨¥”∂¯ø…≤π»´∆µ¬ ∑÷≤º÷±∑ΩÕº£¨≤¢”…∆µ¬ ∑÷≤º÷±∑ΩÕºº∞±Ì∏Ò÷– ˝æðµ√≥ˆ
µƒ∆µ¬ £¨¥”∂¯ø…≤π»´∆µ¬ ∑÷≤º÷±∑ΩÕº£¨≤¢”…∆µ¬ ∑÷≤º÷±∑ΩÕºº∞±Ì∏Ò÷– ˝æðµ√≥ˆ![]() £ª
£ª
£®2£©∏˘æð![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±”Î
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±”Î![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±µƒ»À ˝±»Œ™
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±µƒ»À ˝±»Œ™![]() £¨ΩË÷˙∑÷≤„≥È—˘µƒ∑Ω∑®º¥ø…µ√≥ˆΩ·π˚.
£¨ΩË÷˙∑÷≤„≥È—˘µƒ∑Ω∑®º¥ø…µ√≥ˆΩ·π˚.
£®1£©µ⁄2◊ȵƒ∆µ¬ Œ™![]() £¨À˘“‘–°æÿ–Œµƒ∏þŒ™
£¨À˘“‘–°æÿ–Œµƒ∏þŒ™![]() £¨‘Ú≤π»´µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬£∫
£¨‘Ú≤π»´µƒ∆µ¬ ∑÷≤º÷±∑ΩÕº»Áœ¬£∫
µ⁄1◊È»À ˝Œ™![]() £¨∆µ¬ Œ™
£¨∆µ¬ Œ™![]() £¨À˘“‘
£¨À˘“‘![]() .
.
”÷µ⁄2◊ȵƒ∆µ¬ Œ™0.3£¨π µ⁄2◊È»À ˝Œ™![]() £¨À˘“‘
£¨À˘“‘![]() .
.
µ⁄4◊ȵƒ∆µ¬ Œ™![]() £¨À˘“‘µ⁄4◊È»À ˝Œ™
£¨À˘“‘µ⁄4◊È»À ˝Œ™![]() £¨À˘“‘
£¨À˘“‘![]() .
.
£®2£©“ÚŒ™![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±”Î
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±”Î![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±µƒ»À ˝±»Œ™
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±µƒ»À ˝±»Œ™![]() £¨À˘“‘≤…”√∑÷≤„Àʪ˙≥È—˘µƒ∑Ω∑®≥È»°18»À£¨¥”
£¨À˘“‘≤…”√∑÷≤„Àʪ˙≥È—˘µƒ∑Ω∑®≥È»°18»À£¨¥”![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–”¶≥È»°12»À£¨¥”
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–”¶≥È»°12»À£¨¥”![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–”¶≥È»°6»À.
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–”¶≥È»°6»À.
À˘“‘£¨¿˚”√≥È«©∑®ªÚÀʪ˙ ˝±Ì∑®‘⁄![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°12»À£¨¥”
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°12»À£¨¥”![]() ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°6»À.
ƒÍ¡‰∂Œµƒ°∞µÕú◊°±÷–≥È»°6»À.



 “ª±æ∫√Âø⁄À„Âø®œµ¡–¥∞∏
“ª±æ∫√Âø⁄À„Âø®œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥µÿ«¯ƒ≥≈©≤˙∆∑Ω¸º∏ƒÍµƒ≤˙¡øÕ≥º∆»Áœ¬±Ì:

£®1£©∏˘æð±Ì÷– ˝æð£¨Ω®¡¢![]() πÿ”⁄
πÿ”⁄![]() µƒœþ–‘ªÿπÈ∑Ω≥Ã
µƒœþ–‘ªÿπÈ∑Ω≥Ã![]() £ª
£ª
£®2£©»ÙΩ¸º∏ƒÍ∏√≈©≤˙∆∑√ø«ßøÀµƒº€∏Ò![]() (µ•Œª:‘™£©”΃Í≤˙¡ø
(µ•Œª:‘™£©”΃Í≤˙¡ø![]() ¬˙◊„µƒ∫Ø ˝πÿœµ ΩŒ™
¬˙◊„µƒ∫Ø ˝πÿœµ ΩŒ™![]() £¨«“√øƒÍ∏√≈©≤˙∆∑∂ºƒÐ €ÕÍ.
£¨«“√øƒÍ∏√≈©≤˙∆∑∂ºƒÐ €ÕÍ.
¢Ÿ∏˘æð£®1£©÷–À˘Ω®¡¢µƒªÿπÈ∑Ω≥ѧ≤‚∏√µÿ«¯![]() ƒÍ∏√≈©≤˙∆∑µƒ≤˙¡ø£ª
ƒÍ∏√≈©≤˙∆∑µƒ≤˙¡ø£ª
¢⁄µ±![]() Œ™∫Œ÷µ ±£¨œ˙ €∂Ó
Œ™∫Œ÷µ ±£¨œ˙ €∂Ó![]() ◊Ó¥Û£ø
◊Ó¥Û£ø
∏Ω£∫∂‘”⁄“ª◊È ˝æð![]() £¨∆‰ªÿπÈ÷±œþ
£¨∆‰ªÿπÈ÷±œþ![]() µƒ–±¬ ∫ÕΩÿæýµƒ◊Ó–°∂˛≥Àπ¿º∆∑÷±Œ™£∫
µƒ–±¬ ∫ÕΩÿæýµƒ◊Ó–°∂˛≥Àπ¿º∆∑÷±Œ™£∫ 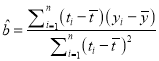 £¨
£¨ ![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £Æ
£Æ
£®1£©µ±![]() ±£¨«Û∫Ø ˝
±£¨«Û∫Ø ˝![]() µƒº´–°÷µ£ª
µƒº´–°÷µ£ª
£®2£©»Ù![]() …œ£¨ πµ√
…œ£¨ πµ√![]() ≥…¡¢£¨«Û
≥…¡¢£¨«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘”⁄œÓ ˝Œ™![]() £®
£®![]() £©µƒ”–«Ó’˝’˚ ˝ ˝¡–
£©µƒ”–«Ó’˝’˚ ˝ ˝¡–![]() ,º«
,º«![]() £®
£®![]() £©£¨º¥
£©£¨º¥![]() Œ™
Œ™![]() ÷–µƒ◊Ó¥Û÷µ£¨≥∆ ˝¡–
÷–µƒ◊Ó¥Û÷µ£¨≥∆ ˝¡–![]() Œ™ ˝¡–
Œ™ ˝¡–![]() µƒ°∞¥¥–¬ ˝¡–°±.±»»Á
µƒ°∞¥¥–¬ ˝¡–°±.±»»Á![]() µƒ°∞¥¥–¬ ˝¡–°±Œ™
µƒ°∞¥¥–¬ ˝¡–°±Œ™![]() .
.
£®1£©»Ù ˝¡–![]() µƒ°∞¥¥–¬ ˝¡–°±
µƒ°∞¥¥–¬ ˝¡–°±![]() Œ™1,2,3,4,4£¨–¥≥ˆÀ˘”–ø…ƒÐµƒ ˝¡–
Œ™1,2,3,4,4£¨–¥≥ˆÀ˘”–ø…ƒÐµƒ ˝¡–![]() £ª
£ª
£®2£©…Ë ˝¡–![]() Œ™ ˝¡–
Œ™ ˝¡–![]() µƒ°∞¥¥–¬ ˝¡–°±£¨¬˙◊„
µƒ°∞¥¥–¬ ˝¡–°±£¨¬˙◊„![]() £®
£®![]() £©£¨«Û÷§£∫
£©£¨«Û÷§£∫ ![]() £®
£®![]() £©£ª
£©£ª
£®3£©…Ë ˝¡–![]() Œ™ ˝¡–
Œ™ ˝¡–![]() µƒ°∞¥¥–¬ ˝¡–°±£¨ ˝¡–
µƒ°∞¥¥–¬ ˝¡–°±£¨ ˝¡–![]() ÷–µƒœÓª•≤ªœýµ»«“À˘”–œÓµƒ∫Õµ»”⁄À˘”–œÓµƒª˝£¨«Û≥ˆÀ˘”–µƒ ˝¡–
÷–µƒœÓª•≤ªœýµ»«“À˘”–œÓµƒ∫Õµ»”⁄À˘”–œÓµƒª˝£¨«Û≥ˆÀ˘”–µƒ ˝¡–![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕºÀ˘ 棨Àƒ±þ–ŒABCD «÷±Ω«Ã𖌣¨![]() £¨
£¨![]() ∆Ω√ÊABCD£¨
∆Ω√ÊABCD£¨![]() £¨
£¨![]() £Æ
£Æ

![]() «ÛSC”Î∆Ω√ÊASDÀ˘≥…µƒΩ«”ýœ“÷µ£ª
«ÛSC”Î∆Ω√ÊASDÀ˘≥…µƒΩ«”ýœ“÷µ£ª
![]() «Û∆Ω√ÊSAB∫Õ∆Ω√ÊSCDÀ˘≥…Ω«µƒ”ýœ“÷µ£Æ
«Û∆Ω√ÊSAB∫Õ∆Ω√ÊSCDÀ˘≥…Ω«µƒ”ýœ“÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£”–![]() °¢
°¢![]() °¢
°¢![]() °¢
°¢![]() Àƒº˛◊˜∆∑≤Œº”∫Ωƒ£¿ý◊˜∆∑±»»¸.“—÷™’‚Àƒº˛◊˜∆∑÷–«°”–¡Ωº˛ªÒΩ±£¨‘⁄Ω·π˚Ω“œ˛«∞£¨º◊°¢““°¢±˚°¢∂°ÀƒŒªÕ¨—ß∂‘’‚Àƒº˛≤Œ»¸◊˜∆∑µƒªÒΩ±«Èøˆ‘§≤‚»Áœ¬.
Àƒº˛◊˜∆∑≤Œº”∫Ωƒ£¿ý◊˜∆∑±»»¸.“—÷™’‚Àƒº˛◊˜∆∑÷–«°”–¡Ωº˛ªÒΩ±£¨‘⁄Ω·π˚Ω“œ˛«∞£¨º◊°¢““°¢±˚°¢∂°ÀƒŒªÕ¨—ß∂‘’‚Àƒº˛≤Œ»¸◊˜∆∑µƒªÒΩ±«Èøˆ‘§≤‚»Áœ¬.
º◊Àµ£∫°∞![]() °¢
°¢![]() Õ¨ ±ªÒΩ±.°±
Õ¨ ±ªÒΩ±.°±
““Àµ£∫°∞![]() °¢
°¢![]() ≤ªø…ƒÐÕ¨ ±ªÒΩ±.°±
≤ªø…ƒÐÕ¨ ±ªÒΩ±.°±
±˚Àµ£∫°∞![]() ªÒΩ±.°±
ªÒΩ±.°±
∂°Àµ£∫°∞![]() °¢
°¢![]() ÷¡…Ÿ“ªº˛ªÒΩ±°±
÷¡…Ÿ“ªº˛ªÒΩ±°±
»Áπ˚“‘…œÀƒŒªÕ¨—ß÷–”–«“÷ª”–¡ΩŒªÕ¨—ßµƒ‘§≤‚ «’˝»∑µƒ£¨‘ÚªÒΩ±µƒ◊˜∆∑ «£® £©
A. ◊˜∆∑![]() ”Î◊˜∆∑
”Î◊˜∆∑![]() B. ◊˜∆∑
B. ◊˜∆∑![]() ”Î◊˜∆∑
”Î◊˜∆∑![]() C. ◊˜∆∑
C. ◊˜∆∑![]() ”Î◊˜∆∑
”Î◊˜∆∑![]() D. ◊˜∆∑
D. ◊˜∆∑![]() ”Î◊˜∆∑
”Î◊˜∆∑![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø√øƒÍµƒΩ«Ô Æ‘¬£¨‘Ω“∞e◊Â∞¢¿≠…∆”¢–€ª·‘⁄ƒ⁄√…π≈◊‘÷Œ«¯∞¢¿≠…∆√À∞¢◊Û∆ÏÃ⁄∏Ò¿Ô…≥ƒÆ柖–£¨∏√œÓƒø“—¥Ú‘Ï≥…ºØ…≥ƒÆæ∫ºº‘À∂Ø°¢∆˚≥µŒƒªØº´÷¬Ã—Ȱ¢÷˜Ã‚–ðœ–∂»ºŸŒ™“ªÃµƒ≥¨º∂∆˚≥µŒƒªØ»¸ ¬”È¿÷◊€∫œÃÂ.Œ™¡Àºı…Ÿ∂‘ª∑æ≥µƒŒ€»æ£¨ƒ≥ª∑±£≤ø√≈◊‚”√¡ÀÃÿ÷∆ª∑±£≥µ«ÂΩýœ÷≥°¿¨ª¯.Õ®π˝≤È‘ƒΩ¸5ƒÍ”¢–€ª·≤Œª·»À ˝![]() £®ÕÚ»À£©”Î…≥ƒÆ÷–À˘–˪∑±£≥µ¡æ ˝¡ø
£®ÕÚ»À£©”Î…≥ƒÆ÷–À˘–˪∑±£≥µ¡æ ˝¡ø![]() £®¡æ£©£¨µ√µΩ»Áœ¬Õ≥º∆±Ì£∫
£®¡æ£©£¨µ√µΩ»Áœ¬Õ≥º∆±Ì£∫
≤Œª·»À ˝ | 11 | 9 | 8 | 10 | 12 |
À˘–˪∑±£≥µ¡æ | 28 | 23 | 20 | 25 | 29 |
£®1£©∏˘æðÕ≥º∆±ÌÀ˘∏¯5◊È ˝æ𣨫Û≥ˆ![]() πÿ”⁄
πÿ”⁄![]() µƒœþ–‘ªÿπÈ∑Ω≥Ã
µƒœþ–‘ªÿπÈ∑Ω≥Ã![]() £Æ
£Æ
£®2£©“—÷™◊‚”√µƒª∑±£≥µ∆Ωæ˘√ø¡æµƒ∑—”√![]() £®‘™£©”Î ˝¡ø
£®‘™£©”Î ˝¡ø![]() £®¡æ£©µƒπÿœµŒ™
£®¡æ£©µƒπÿœµŒ™
![]() .÷˜∞Ï∑Ω∏˘æ𠵺 ≤Œª·»À ˝Œ™À˘–Ë“™Õ∂»Î π”√µƒª∑±£≥µ£¨
.÷˜∞Ï∑Ω∏˘æ𠵺 ≤Œª·»À ˝Œ™À˘–Ë“™Õ∂»Î π”√µƒª∑±£≥µ£¨
√ø¡æ÷ß∏∂∑—”√6000‘™£¨≥¨≥ˆ µº –Ë“™µƒ≥µ¡æ£¨÷˜∞Ï∑Ω≤ª÷ß∏∂»Œ∫Œ∑—”√.‘§º∆±æ¥Œ”¢–€ª·¥Û‘º”–14ÕÚ»À≤Œº”£¨∏˘æ𣮢ң©÷–«Û≥ˆµƒœþ–‘ªÿπÈ∑Ω≥㨑§≤‚ª∑±£≤ø√≈‘⁄»∑±£«ÂΩý»ŒŒÒÕÍ≥…µƒ«∞÷œ¬£¨”¶◊‚”√∂ý…Ÿ¡æª∑±£≥µ£øªÒµ√µƒ¿˚»Û![]() «∂ý…Ÿ£ø£®◊¢£∫¿˚»Û
«∂ý…Ÿ£ø£®◊¢£∫¿˚»Û![]() ÷˜∞Ï∑Ω÷ß∏∂∑—”√
÷˜∞Ï∑Ω÷ß∏∂∑—”√![]() ◊‚”√≥µ¡æµƒ∑—”√£©£Æ
◊‚”√≥µ¡æµƒ∑—”√£©£Æ
≤Œøºπ´ Ω£∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…Ë![]() «
«![]() ‘⁄µ„
‘⁄µ„![]() ¥¶µƒ«–œþ£Æ
¥¶µƒ«–œþ£Æ
£®![]() £©«Û
£©«Û![]() µƒΩ‚Œˆ Ω£Æ
µƒΩ‚Œˆ Ω£Æ
£®![]() £©«Û÷§£∫
£©«Û÷§£∫ ![]() £Æ
£Æ
£®![]() £©…Ë
£©…Ë![]() £¨∆‰÷–
£¨∆‰÷–![]() £Æ»Ù
£Æ»Ù![]() ∂‘
∂‘![]() ∫„≥…¡¢£¨«Û
∫„≥…¡¢£¨«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
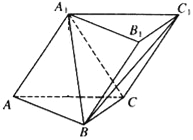
°æƒø°ø»ÁÕº£¨»˝¿‚÷˘ABC©ÅA1B1C1÷–£¨≤ý√ÊAA1C1C°Õµ◊√ÊABC£¨AA1=A1C=AC=2£¨AB=BC«“AB°ÕBC£¨
£®¢Ò£©«Û÷§£∫AC°ÕA1B£ª
£®¢Ú£©«Û∂˛√ÊΩ«A©ÅA1C©ÅBµƒ”ýœ“÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com