
 的一个极值点,
的一个极值点,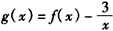 ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。  第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:甘肃省张掖二中2012届高三9月月考数学文科试题 题型:022
给出下列命题
(1)已知直线m,l,平面α,β,若![]() ,则
,则![]()
(2)![]() ,是
,是![]() 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
(3)如果函数y=f(x)为奇函数,则f(0)=0
(4)若![]() ,则f(x0)为极大值或极小值
,则f(x0)为极大值或极小值
(5)![]() 的图象的一个对称中心是
的图象的一个对称中心是![]()
以上命题正确的是________(注:把你认为正确的命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
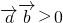 ,是
,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;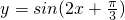 的图象的一个对称中心是
的图象的一个对称中心是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com