【答案】
分析:根据函数定义域求法,可得①是真命题;根据幂函数与指数函数的值域求法,可得②是假命题;根据函数奇偶性的定义,用比较系数法加以验证可得③当中应该是充要条件,故不正确;根据二次函数与指数函数的图象与性质,得到④不正确.由此得到本题的答案.
解答:解:由于y=a
x(a>0且a≠1)与函数y=log
a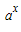
(a>0且a≠1)的定义域都是R,
所以①是真命题;
由于函数y=x
3的值域是R,而函数y=3
x的值域是(0,+∞)
所以y=x
3与y=3
x的值域不相同,可得②是假命题;
对于③,当a=1时,函数f(x)=
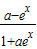
即
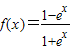
,满足f(-x)=
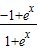
=-f(x)是奇函数;
反之若f(x)=
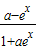
是奇函数,由f(-x)=-f(x)比较系数得a=-1
故“a=1”是“函数f(x)=
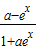
是在定义域上的奇函数”的充要条件,可得③是假命题;
对于④,二次函数y=(x-1)
2在区间[0,1)上是减函数,在区间(1,+∞)上是增函数
y=2
x-1在区间[0,+∞)上是增函数
因此y=(x-1)
2与y=2
x-1在区间[0,+∞)上都不是减函数,得④不正确
综上所述,其中的正确命题是①
故答案为:①
点评:本题由几个命题的真假判断,考查了二次函数、幂函数与指对数函数的图象与性质,函数的单调性与奇偶性等知识,属于中档题.

 (a>0且a≠1)的定义域相同;
(a>0且a≠1)的定义域相同; 是在定义域上的奇函数”的充分不必要条件;
是在定义域上的奇函数”的充分不必要条件;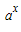 (a>0且a≠1)的定义域都是R,
(a>0且a≠1)的定义域都是R,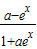 即
即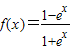 ,满足f(-x)=
,满足f(-x)=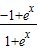 =-f(x)是奇函数;
=-f(x)是奇函数;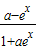 是奇函数,由f(-x)=-f(x)比较系数得a=-1
是奇函数,由f(-x)=-f(x)比较系数得a=-1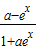 是在定义域上的奇函数”的充要条件,可得③是假命题;
是在定义域上的奇函数”的充要条件,可得③是假命题;

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案