
ΓΨΧβΡΩΓΩ»γΆΦΘ§…ψ”ΑΑ°ΚΟ’Ώ‘ΎΡ≥ΙΪ‘ΑA¥ΠΘ§ΖΔœ÷’ΐ«ΑΖΫB¥Π”–“ΜΝΔ÷υΘ§≤βΒΟΝΔ÷υΕΞΕΥOΒΡ―ωΫ«ΚΆΝΔ÷υΒΉ≤ΩBΒΡΗ©Ϋ«ΨυΈΣ![]() Θ§“―÷Σ…ψ”ΑΑ°ΚΟ’ΏΒΡ…μΗΏ‘ΦΈΣ
Θ§“―÷Σ…ψ”ΑΑ°ΚΟ’ΏΒΡ…μΗΏ‘ΦΈΣ![]() ΟΉΘ®ΫΪ―έΨΠSΨύΒΊΟφΒΡΨύάκSAΑ¥
ΟΉΘ®ΫΪ―έΨΠSΨύΒΊΟφΒΡΨύάκSAΑ¥![]() ΟΉ¥ΠάμΘ©Θ°
ΟΉ¥ΠάμΘ©Θ°
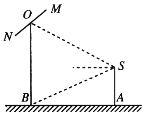
Θ®1Θ©«σ…ψ”ΑΑ°ΚΟ’ΏΒΫΝΔ÷υΒΡΥ°ΤΫΨύάκABΚΆΝΔ÷υΒΡΗΏΕ»OBΘΜ
Θ®2Θ©ΝΔ÷υΒΡΕΞΕΥ”–“Μ≥ΛΈΣ2ΟΉΒΡ≤ ΗΥMNΘ§«“MN»ΤΤδ÷–ΒψO‘Ύ…ψ”ΑΑ°ΚΟ’Ώ”κΝΔ÷υΥυ‘ΎΒΡΤΫΟφΡΎ–ΐΉΣΘ°‘Ύ≤ ΗΥΉΣΕ·ΒΡ»Έ“β ±ΩΧΘ§…ψ”ΑΑ°ΚΟ’ΏΙέ≤λ≤ ΗΥMNΒΡ ”Ϋ«![]() Θ®…ηΈΣ
Θ®…ηΈΣ![]() Θ© «Ζώ¥φ‘ΎΉν¥σ÷ΒΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω
Θ© «Ζώ¥φ‘ΎΉν¥σ÷ΒΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω![]() »ΓΉν¥σ÷Β ±
»ΓΉν¥σ÷Β ±![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩ(1) ABΈΣ3ΟΉ OBΈΣ2![]() ΟΉ (2) Β± ”Ϋ«ΓœMSN»ΓΉν¥σ÷Β ±,cosΠ»=
ΟΉ (2) Β± ”Ϋ«ΓœMSN»ΓΉν¥σ÷Β ±,cosΠ»=![]() .
.
ΓΨΫβΈωΓΩ
(1)»γΆΦ,ΉςSCΓΆOB”ΎC,
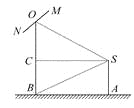
“άΧβ“βΓœCSB=30Γψ,ΓœASB=60Γψ.
”÷SA=![]() ,Ι ‘ΎRtΓςSAB÷–,Ω…«σΒΟAB=
,Ι ‘ΎRtΓςSAB÷–,Ω…«σΒΟAB=![]() =3,
=3,
Φ¥…ψ”ΑΑ°ΚΟ’ΏΒΫΝΔ÷υΒΡΥ°ΤΫΨύάκABΈΣ3ΟΉ.
‘ΎRtΓςSCO÷–,SC=3,ΓœCSO=30Γψ,OC=SCΓΛtan 30Γψ=![]() ,
,
”÷BC=SA=![]() ,Ι OB=2
,Ι OB=2![]() ,Φ¥ΝΔ÷υΒΡΗΏΕ»OBΈΣ2
,Φ¥ΝΔ÷υΒΡΗΏΕ»OBΈΣ2![]() ΟΉ.
ΟΉ.
(2)ΖΫΖ®“Μ:»γΆΦ,“‘OΈΣ‘≠Βψ,“‘Υ°ΤΫΖΫœρœρ”“ΈΣx÷α’ΐΖΫœρΫ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒ,Ν§Ϋ”SM,SN,
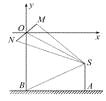
…ηM(cosΠΝ,sinΠΝ),ΠΝΓ [0,2Π–),
‘ρN(-cosΠΝ,-sinΠΝ),”…(1)÷ΣS(3,-![]() ).
).
Ι ![]() =(cosΠΝ-3,sinΠΝ+
=(cosΠΝ-3,sinΠΝ+![]() ),
),
![]() =(-cosΠΝ-3,-sinΠΝ+
=(-cosΠΝ-3,-sinΠΝ+![]() ),
),
ΓΏ![]() ΓΛ
ΓΛ![]() =(cosΠΝ-3)ΓΛ(-cosΠΝ-3)+(sinΠΝ+
=(cosΠΝ-3)ΓΛ(-cosΠΝ-3)+(sinΠΝ+![]() )ΓΛ(-sinΠΝ+
)ΓΛ(-sinΠΝ+![]() )=11.
)=11.
|![]() |ΓΛ|
|ΓΛ|![]() |=
|=![]() ΓΛ
ΓΛ
![]()
=![]() ΓΛ
ΓΛ
![]()
=![]()
=![]() .
.
”…ΠΝΓ [0,2Π–)÷Σ|![]() |ΓΛ|
|ΓΛ|![]() |Γ [11,13].
|Γ [11,13].
Υυ“‘cosΓœMSN=![]() Γ [
Γ [![]() ,1],“Ή÷ΣΓœMSNΈΣ»ώΫ«,
,1],“Ή÷ΣΓœMSNΈΣ»ώΫ«,
Ι Β± ”Ϋ«ΓœMSN»ΓΉν¥σ÷Β ±,cosΠ»=![]() .
.
ΖΫΖ®Εΰ:ΓΏcosΓœMOS=-cosΓœNOS,
Γύ![]() =-
=-![]()
”Ύ «ΒΟSM2+SN2=26¥”Εχ
cosΠ»=![]() Γί
Γί![]() =
=![]() .
.
”÷ΓœMSNΈΣ»ώΫ«,
Ι Β± ”Ϋ«ΓœMSN»ΓΉν¥σ÷Β ±,cosΠ»=![]() .
.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ2018Ρξ10‘¬19»’Θ§”…÷–ΙζΙΛ–≈≤ΩΓΔΫ≠Ές Γ’ΰΗ°ΝΣΚœ÷ςΑλΒΡ άΫγVRΘ®–ιΡβœ÷ ΒΘ©≤ζ“Β¥σΜα‘ΎΡœ≤ΐΩΣΡΜΘ§Ρœ≤ΐ‘ΎΚλΙ»Χ≤–¬«χΫ®ΝΔVRΧΊ…Ϊ–Γ’ρœνΡΩΘ°œ÷Ρ≥≥ß…ΧΉΞΉΓ…ΧΜζ‘Ύ»ΞΡξ”Ο450Άρ‘ΣΙΚΫχ“Μ≈ζVR…η±ΗΘ§Ψ≠Βς ‘ΚσΫώΡξΆΕ»κ Ι”ΟΘ§ΦΤΜ°ΒΎ“ΜΡξΈ§–όΓΔ±Θ―χΖ―”Ο22Άρ‘ΣΘ§¥”ΒΎΕΰΡξΩΣ ΦΘ§ΟΩΡξΥυ–ηΈ§–όΓΔ±Θ―χΖ―”Ο±»…œ“ΜΡξ‘ωΦ”4Άρ‘ΣΘ§ΗΟ…η±Η Ι”ΟΚσΘ§ΟΩΡξΒΡΉή ’»κΈΣ180Άρ‘ΣΘ§…η Ι”ΟxΡξΚσ…η±ΗΒΡ”·άϊΕνΈΣyΆρ‘ΣΘ°
Θ®1Θ©–¥≥ωy”κx÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ© Ι”Ο»τΗ…ΡξΚσΘ§Β±ΡξΤΫΨυ”·άϊΕν¥οΒΫΉν¥σ÷Β ±Θ§«σΗΟ≥ß…ΧΒΡ”·άϊΕν.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΝ…ΡΰΚ≈ΚΫΡΗΦΆΡν’¬¥”2012Ρξ10‘¬5»’ΤπΩΣ Φ…œ –Θ§Ά®Ιΐ –≥ΓΒς≤ιΘ§ΒΟΒΫΗΟΦΆΡν’¬ΟΩ![]() ΟΕΒΡ –≥ΓΦέ
ΟΕΒΡ –≥ΓΦέ![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©”κ…œ – ±Φδ
Θ®ΒΞΈΜΘΚ‘ΣΘ©”κ…œ – ±Φδ![]() Θ®ΒΞΈΜΘΚΧλΘ©ΒΡ ΐΨί»γœ¬ΘΚ
Θ®ΒΞΈΜΘΚΧλΘ©ΒΡ ΐΨί»γœ¬ΘΚ
…œ – ±Φδ |
|
|
|
–≥ΓΦέ |
|
|
|
Θ®1Θ©ΗυΨί…œ±μ ΐΨίΘ§¥”œ¬Ν–Κ· ΐ÷–―ûÓΜΗω«ΓΒ±ΒΡΚ· ΐΟη ωΝ…ΡΰΚ≈ΚΫΡΗΦΆΡν’¬ΒΡ –≥ΓΦέ![]() ”κ…œ – ±Φδ
”κ…œ – ±Φδ![]() ΒΡ±δΜ·ΙΊœΒΘΚΔΌ
ΒΡ±δΜ·ΙΊœΒΘΚΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() ΘΜΔέ
ΘΜΔέ![]() ΘΜ
ΘΜ
Θ®2Θ©άϊ”ΟΡψ―Γ»ΓΒΡΚ· ΐΘ§«σΝ…ΡΰΚ≈ΚΫΡΗΦΆΡν’¬ –≥ΓΦέΉνΒΆ ±ΒΡ…œ –Χλ ΐΦΑΉνΒΆΒΡΦέΗώΘΜ
Θ®3Θ©…ηΡψ―Γ»ΓΒΡΚ· ΐΈΣ![]() Θ§»τΕ‘»Έ“β Β ΐ
Θ§»τΕ‘»Έ“β Β ΐ![]() Θ§ΙΊ”Ύ
Θ§ΙΊ”Ύ![]() ΒΡΖΫ≥Χ
ΒΡΖΫ≥Χ![]() Κψ”–Ηωœκ“λ Β ΐΗυΘ§«σ
Κψ”–Ηωœκ“λ Β ΐΗυΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ’ΐœν ΐΝ–¬ζΉψ4Sn=Θ®an+1Θ©2 Θ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΙΪ ΫΘΜ
Θ®2Θ©…ηbn=![]() Θ§ «σ ΐΝ–{bn}ΒΡ«ΑnœνΚΆTn Θ°
Θ§ «σ ΐΝ–{bn}ΒΡ«ΑnœνΚΆTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΈΣ
ΒΡ±ξΉΦΖΫ≥ΧΈΣ![]() Θ§
Θ§![]() ΈΣ‘≤
ΈΣ‘≤![]() …œΒΡΕ·ΒψΘ§÷±œΏ
…œΒΡΕ·ΒψΘ§÷±œΏ![]() ΒΡΖΫ≥ΧΈΣ
ΒΡΖΫ≥ΧΈΣ![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ‘Ύ÷±œΏ
‘Ύ÷±œΏ![]() …œΘ°
…œΘ°
Θ®1Θ©«σ![]() ΒΡΉν–Γ÷ΒΘ§≤Δ«σ¥Υ ±Βψ
ΒΡΉν–Γ÷ΒΘ§≤Δ«σ¥Υ ±Βψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
Θ®2Θ©»τ![]() ΒψΒΡΉχ±ξΈΣ
ΒψΒΡΉχ±ξΈΣ![]() Θ§Ιΐ
Θ§Ιΐ![]() Ής÷±œΏ”κ‘≤
Ής÷±œΏ”κ‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§Β±
ΝΫΒψΘ§Β±![]() ±Θ§«σ÷±œΏ
±Θ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘ°
ΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘≤–Ρ‘Ύy÷α…œΘ§ΑκΨΕΈΣ1Θ§«“ΙΐΒψΘ®1Θ§2Θ©ΒΡ‘≤ΒΡΖΫ≥ΧΈΣΘ®ΓΓΓΓΘ©
A.x2+Θ®y©¹2Θ©2=1
B.x2+Θ®y+2Θ©2=1
C.Θ®x©¹1Θ©2+Θ®y©¹3Θ©2=1
D.x2+Θ®y©¹3Θ©2=1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() ΤδΆΦœώΒΡ“ΜΗωΕ‘≥Τ÷––Ρ «
ΤδΆΦœώΒΡ“ΜΗωΕ‘≥Τ÷––Ρ «![]() ΫΪ
ΫΪ![]() ΒΡΆΦœώœρΉσΤΫ“Τ
ΒΡΆΦœώœρΉσΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»ΚσΒΟΒΫΚ· ΐ
ΗωΒΞΈΜ≥ΛΕ»ΚσΒΟΒΫΚ· ΐ![]() ΒΡΆΦœώΓΘ
ΒΡΆΦœώΓΘ
(1)«σΚ· ΐ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
(2)»τΕ‘»Έ“β![]() Β±
Β±![]() ±Θ§ΕΦ”–
±Θ§ΕΦ”–![]() «σ Β ΐ
«σ Β ΐ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
(3)»τΕ‘»Έ“β Β ΐ![]() ‘Ύ
‘Ύ![]() …œ”κ÷±œΏ
…œ”κ÷±œΏ![]() ΒΡΫΜΒψΗω ΐ≤Μ…Ό”Ύ6Ηω«“≤ΜΕύ”Ύ10ΗωΘ§«σ’ΐ Β ΐ
ΒΡΫΜΒψΗω ΐ≤Μ…Ό”Ύ6Ηω«“≤ΜΕύ”Ύ10ΗωΘ§«σ’ΐ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΓΘ
ΒΡ»Γ÷ΒΖΕΈßΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥≤ζΤΖ…ζ≤ζ≥ßΦ“ΗυΨί“‘ΆυΒΡ…ζ≤ζœζ έΨ≠―ιΒΟΒΫœ¬Οφ”–ΙΊ…ζ≤ζœζ έΒΡΆ≥ΦΤΙφ¬…ΘΚΟΩ…ζ≤ζ≤ζΤΖ![]() Θ®ΑΌΧ®Θ©Θ§ΤδΉή≥…±ΨΈΣ
Θ®ΑΌΧ®Θ©Θ§ΤδΉή≥…±ΨΈΣ![]() Θ®Άρ‘ΣΘ©Θ§Τδ÷–ΙΧΕ®≥…±ΨΈΣ
Θ®Άρ‘ΣΘ©Θ§Τδ÷–ΙΧΕ®≥…±ΨΈΣ![]() Άρ‘ΣΘ§≤Δ«“ΟΩ…ζ≤ζ
Άρ‘ΣΘ§≤Δ«“ΟΩ…ζ≤ζ![]() ΑΌΧ®ΒΡ…ζ≤ζ≥…±ΨΈΣ
ΑΌΧ®ΒΡ…ζ≤ζ≥…±ΨΈΣ![]() Άρ‘ΣΘ®Ήή≥…±Ψ
Άρ‘ΣΘ®Ήή≥…±Ψ![]() ΙΧΕ®≥…±Ψ
ΙΧΕ®≥…±Ψ![]() …ζ≤ζ≥…±ΨΘ©Θ°œζ έ ’»κ
…ζ≤ζ≥…±ΨΘ©Θ°œζ έ ’»κ![]() Θ®Άρ‘ΣΘ©¬ζΉψ
Θ®Άρ‘ΣΘ©¬ζΉψ![]() Θ§ΦΌΕ®ΗΟ≤ζΤΖ≤ζœζΤΫΚβΘ®Φ¥…ζ≤ζΒΡ≤ζΤΖΕΦΡή¬τΒτΘ©Θ§ΗυΨί…œ ωΆ≥ΦΤΙφ¬…Θ§«κΆξ≥…œ¬Ν–Έ ΧβΘΚ
Θ§ΦΌΕ®ΗΟ≤ζΤΖ≤ζœζΤΫΚβΘ®Φ¥…ζ≤ζΒΡ≤ζΤΖΕΦΡή¬τΒτΘ©Θ§ΗυΨί…œ ωΆ≥ΦΤΙφ¬…Θ§«κΆξ≥…œ¬Ν–Έ ΧβΘΚ
Θ®1Θ©–¥≥ωάϊ»σΚ· ΐ![]() ΒΡΫβΈω ΫΘ®άϊ»σ
ΒΡΫβΈω ΫΘ®άϊ»σ![]() œζ έ ’»κ
œζ έ ’»κ![]() Ήή≥…±ΨΘ©ΘΜ
Ήή≥…±ΨΘ©ΘΜ
Θ®2Θ©ΙΛ≥ß…ζ≤ζΕύ…ΌΧ®≤ζΤΖ ±Θ§Ω… Ι”·άϊΉνΕύΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΙΊ”ΎΚ· ΐ![]() ΒΡ≈–Εœ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
ΒΡ≈–Εœ’ΐ»ΖΒΡ «Θ®ΓΓΓΓΘ©
ΔΌ![]() ΒΡΫβΦ· «
ΒΡΫβΦ· «![]() ΘΜ
ΘΜ
ΔΎ![]() ΦΪ–Γ÷ΒΘ§
ΦΪ–Γ÷ΒΘ§![]() «ΦΪ¥σ÷ΒΘΜ
«ΦΪ¥σ÷ΒΘΜ
Δέ![]() ΟΜ”–Ήν–Γ÷ΒΘ§“≤ΟΜ”–Ήν¥σ÷ΒΘ°
ΟΜ”–Ήν–Γ÷ΒΘ§“≤ΟΜ”–Ήν¥σ÷ΒΘ°
A. ΔΌΔέ B. ΔΌΔΎΔέ C. ΔΎ D. ΔΌΔΎ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com