
 的首项
的首项 ,
, 是
是 的前
的前 项和,且
项和,且
 .
. ,求数列
,求数列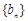 的通项公式;
的通项公式; ,证明:
,证明: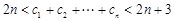 ,
, .
.科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
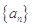 的首项
的首项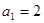 ,且对任意
,且对任意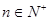 都有
都有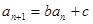 (其中
(其中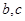 为常数).
为常数).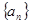 为等差数列,且
为等差数列,且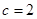 ,求
,求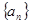 的通项公式.
的通项公式.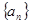 是等比数列,且
是等比数列,且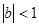 ,从数列
,从数列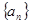 中任意取出相邻的三项,均能按某种顺序排成等差数列,求
中任意取出相邻的三项,均能按某种顺序排成等差数列,求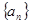 的前
的前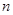 项和
项和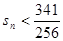 成立的
成立的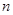 的取值的集合.
的取值的集合.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
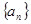 的各项均为正数,且
的各项均为正数,且
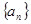 的通项公式;
的通项公式;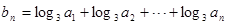 ,求数列
,求数列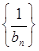 的前n项和
的前n项和 ;
;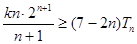 恒成立的实数
恒成立的实数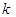 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
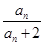 (n∈N*).若bn+1=(n-λ)(
(n∈N*).若bn+1=(n-λ)(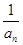 +1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )
+1)(n∈N*),b1=-λ,且数列{bn}是单调递增数列,则实数λ的取值范围为( )| A.λ>2 | B.λ>3 | C.λ<2 | D.λ<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com