练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

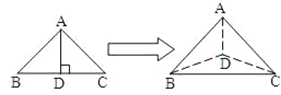
    【题目】如图，以等腰直角三角形斜边BC上的高AD为折痕，把△ABD和△ACD折成互相垂直的两个平面后，某学生得出下列四个结论：

    ①；

    ②∠BAC=60°；

    ③三棱锥D﹣ABC是正三棱锥；

    ④平面ADC和平面ABC的垂直．

    其中正确的是（　 　）

    A. ①② B. ②③ C. ③④ D. ①④

    【答案】B

    【解析】

    ①由折叠的原理，可知BD⊥平面ADC，可推知BD⊥AC，数量积为零，②因为折叠后AB=AC=BC，三角形为等边三角形，所以∠BAC=60°；③又因为DA=DB=DC，根据正三棱锥的定义判断．④平面ADC和平面ABC不垂直．

    BD⊥平面ADCBD⊥AC，①错；

    AB=AC=BC，②对；

    DA=DB=DC，结合②，③对④错．

    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，AB＝BC＝4，点E在线段AB上．过点E作EF∥BC交AC于点F，将△AEF沿EF折起到△PEF的位置(点A与P重合)，使得∠PEB＝60°.

    (1)求证：EF⊥PB.

    (2)试问：当点E在线段AB上移动时，二面角PFCB的平面角的余弦值是否为定值？若是，求出其定值；若不是，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分14分）

    如图1，在三棱锥P－ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上一点，它的正(主)视图和侧(左)视图如图2所示．

    (1) 证明：AD⊥平面PBC；

    (2) 在∠ACB的平分线上确定一点Q，使得PQ∥平面ABD，并求此时PQ的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，，动点满足．

    (1)求动点的轨迹的方程；

    (2)设点为轨迹上异于原点的两点，且．

    ①若为常数，求证：直线过定点；

    ②求轨迹上任意一点到①中的点距离的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线过椭圆的右焦点且与椭圆交于两点， 为中点， 的斜率为.

    （1）求椭圆的方程；

    （2）设是椭圆的动弦，且其斜率为1，问椭圆上是否存在定点，使得直线的斜率满足？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4 ， 坐标系与参数方程]
    在直角坐标系xOy中，曲线C的参数方程为 （θ为参数），直线l的参数方程为 （t为参数）．（10分）
    （1）若a=﹣1，求C与l的交点坐标；
    （2）若C上的点到l距离的最大值为 ，求a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】命题p：关于x的方程x2＋ax＋2＝0无实根，命题q：函数f(x)＝logax在(0，＋∞)上单调递增，若“p∧q”为假命题，“p∨q”真命题，求实数a的取值范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列五个命题：

    ①当时，有；

    ②若是锐角三角形，则；

    ③已知是等差数列的前项和，若，则；

    ④函数与的图像关于直线对称；

    ⑤当时，不等式恒成立，则实数的取值范围为.

    其中正确命题的序号为___________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C1:y2=2x与C2:y=x2在第一象限内的交点为P.

    (1)求过点P且与曲线C2相切的直线方程;

    (2)求两条曲线所围图形(如图所示的阴影部分)的面积S.

    查看答案和解析>>

    同步练习册答案