
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,上项点为B,M(1,0),N(n,0),|MB|=$\sqrt{2}$,|AM|=3.过点M作直线l(与x轴不重合),直线l与椭圆C相交于P,Q两点,且有NP⊥NQ.分析 (Ⅰ)由条件M(1,0),|MB|=$\sqrt{2}$,可知b=1,再由|AM|=3,可得a=2,进而得到椭圆方程;
(Ⅱ)讨论当直线l斜率不存在时,直线的斜率垂直,求出直线方程,联立椭圆方程,运用韦达定理和向量垂直的条件:数量积为0,解不等式可得a的范围.
解答 解:(Ⅰ)B为上项点,M(1,0),|MB|=$\sqrt{2}$,可知b=1,
又|AM|=3,且左顶点为A,所以a=2,
所以椭圆方程为$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)当直线l斜率不存在时,方程为x=1,易得P(1,$\frac{\sqrt{3}}{2}$),Q(1,-$\frac{\sqrt{3}}{2}$),
因为NP⊥NQ,所以N在以M为圆心,$\frac{\sqrt{3}}{2}$为半径的圆上,又N(n,0),
所以可得n=1-$\frac{\sqrt{3}}{2}$或n=1+$\frac{\sqrt{3}}{2}$;
当直线l斜率存在且不为0时,设方程为y=k(x-1),联立$\frac{{x}^{2}}{4}$+y2=1可得,
(1+4k2)x2-8k2x+4k2-4=0,
设P(x1,y1),Q(x2,y2),所以x1+x2=$\frac{8{k}^{2}}{1+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-4}{1+4{k}^{2}}$,(*)
因为NP⊥NQ,所以$\overrightarrow{NP}$•$\overrightarrow{NQ}$=0,即(x1-n)(x2-n)+y1y2=0,
所以(1+k2)x1x2-(n+k2)(x1+x2)+n2+k2=0,
将(*)式代入整理得(4n2-8n+1)k2+n2-4=0,
所以k2=$\frac{4-{n}^{2}}{4{n}^{2}-8n+1}$>0,可得-2<n<1-$\frac{\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$<n<2;
综上可知:-2<n≤1-$\frac{\sqrt{3}}{2}$或1+$\frac{\sqrt{3}}{2}$≤n<2.
点评 本题考查椭圆方程的求法,考查直线和椭圆的位置关系,注意联立直线方程和椭圆方程,运用韦达定理,以及向量垂直的条件:数量积为0,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元).
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需要维修),其他三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y(单位:元).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}\sqrt{2}$ | B. | $14\sqrt{2}$ | C. | $7\sqrt{2}$ | D. | $\frac{7}{3}\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
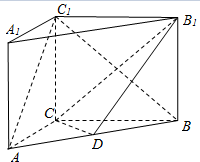 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,CC1⊥底面ABC,AC⊥CB,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,CC1⊥底面ABC,AC⊥CB,点D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com