解:(1)甲队中的3人答题可看做3次独立重复试验.
事件A:甲队一人答题答对,
则P(A)=

,
又答对得1分,答错得0分,
∴甲队的总分ξ~(3,

),
∴P(ξ=0)=

,P(ξ=1)=
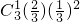
=

,
P(ξ=2)=

,P(ξ=3)=
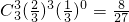
.
∴分布列为

∴Eξ=3×

=2;
(2)事件AB:甲乙两队得分之和为3分,且甲队得分大于乙队得分,
所以,事件AB包括甲队得3分,乙队得0分;甲队得2分,乙队得1分,
∵乙队中3人答对的概率分别为

,

,

,∴乙队中3人答错的概率分别为
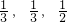
.
∴P(AB)=

+

×[

×

×

+

×

×

+

]
=

.
所以,P(AB)=

.
分析:(1)甲队中的3名同学各自独立的回答一个问题,且答对的概率均为

,所以可以理解为进行3次独立重复试验,3名同学答题得分的所有可能为0、1、2、3,利用独立重复试验的概率公式求出ξ分别是0、1、2、3时的概率,则ξ的分布列可求,数学期望可直接利用二项分布的期望公式求解;
(2)事件A“甲乙两队总分之和等于3”,事件B“甲队总分大于乙队总分”,则事件AB所包含的情况为:“甲队得3分,乙队得0分”;“甲队得2分,乙队得1分”,两类情况为互斥事件,每一类的概率可用相互独立事件的概率求解.
点评:本题考查了n次独立重复试验恰有k次发生的概率,训练了离散型随机变量的分布列的求解,考查了二项分布的期望公式,考查了互斥事件的概率等于概率和,练习相互独立事件的概率的求法,是中档题.

 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,
, ,
, .且每个人回答正确与否互不影响,用ξ表示甲队的总分.
.且每个人回答正确与否互不影响,用ξ表示甲队的总分. ,
, ),
), ,P(ξ=1)=
,P(ξ=1)=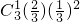 =
= ,
, ,P(ξ=3)=
,P(ξ=3)=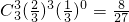 .
.
 =2;
=2;  ,
, ,
, ,∴乙队中3人答错的概率分别为
,∴乙队中3人答错的概率分别为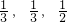 .
. +
+ ×[
×[ ×
× ×
× +
+ ×
× ×
× +
+ ]
] .
. .
. ,所以可以理解为进行3次独立重复试验,3名同学答题得分的所有可能为0、1、2、3,利用独立重复试验的概率公式求出ξ分别是0、1、2、3时的概率,则ξ的分布列可求,数学期望可直接利用二项分布的期望公式求解;
,所以可以理解为进行3次独立重复试验,3名同学答题得分的所有可能为0、1、2、3,利用独立重复试验的概率公式求出ξ分别是0、1、2、3时的概率,则ξ的分布列可求,数学期望可直接利用二项分布的期望公式求解;

 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ,
, ,
, .且每个人回答正确与否互不影响,用ξ表示甲队的总分.
.且每个人回答正确与否互不影响,用ξ表示甲队的总分.