练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    用反证法证明命题：“若，那么，，中至少有一个不小于”时，反设正确的是(     )
    A．假设，，至多有两个小于
    B．假设，，至多有一个小于
    C．假设，，都不小于
    D．假设，，都小于
    D

    试题分析：根据题意，由于反证法证明命题:“若，那么，，中至少有一个不小于”时，即将结论变为否定就是对命题的反设，因此可知至少有一个的否定是一个也没有，或者说假设，，都小于，故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    已知x∈R，a＝x2＋，b＝2－x，c＝x2－x＋1，试证明a，b，c至少有一个不小于1.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    设是一个自然数，是的各位数字的平方和，定义数列：是自然数，（，）．
    （1）求，；
    （2）若，求证：；
    （3）当时，求证：存在，使得．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知数列{an}满足a1＝λ，an＋1＝an＋n－4，λ∈R，n∈N＋，对任意λ
    ∈R，证明：数列{an}不是等比数列．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

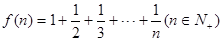    已知．经计算得，，，，，通过观察，我们可以得到一个一般性的结论．
    （1）试写出这个一般性的结论；
    （2）请用数学归纳法证明这个一般性的结论；
    （3）对任一给定的正整数，试问是否存在正整数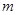，使得？
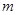    若存在，请给出符合条件的正整数的一个值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    边长为a的正三角形内任一点到三边距离之和为定值
    		3
    2
    a    ，类比到空间，棱长均为a的三棱锥内任一点到各面距离之和为（　　）
    A．
    		3
    a
    3
    		B．
    		6
    a
    2
    		C．
    		6
    a
    3
    		D．
    		2
    a
    2

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    用反证法证明命题“三角形的内角至多有一个钝角”时，假设的内容应为（ ）
    A．假设至少有一个钝角B．假设至少有两个钝角
    C．假设没有一个钝角D．假设没有一个钝角或至少有两个钝角

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

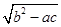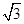    分析法又称执果索因法，若用分析法证明：“设a>b>c，且a＋b＋c＝0，求证 <a”索的因应是(　　)
    A．a－b>0B．a－c>0
    C．(a－b)(a－c)>0D．(a－b)(a－c)<0

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    用反证法证明“自然数a，b，c中恰有一个偶数”时，下列假设正确的是   （   ）
    A．假设a，b，c都是奇数或至少有两个偶数
    B．假设a，b，c都是偶数
    C．假设a，b，c至少有两个偶数
    D．假设a， b，c都是奇数

    查看答案和解析>>

    同步练习册答案