在平面直角坐标系xOy中,O是坐标原点,设函数f(x)=k(x-2)+3的图象为直线l,且l与x轴、y轴分别交于A、B两点,给出下列四个命题:
①存在正实数m,使△AOB的面积为m的直线l仅有一条;
②存在正实数m,使△AOB的面积为m的直线l仅有两条;
③存在正实数m,使△AOB的面积为m的直线l仅有三条;
④存在正实数m,使△AOB的面积为m的直线l仅有四条.
其中所有真命题的序号是( )
A.①②③
B.③④
C.②④
D.②③④
【答案】
分析:根据直线方程求出直线在两坐标轴上的截距,再构造以斜率k为自变量,S
△是变量k的函数,利用均值不等式求函数最小值方法,分k>0和k<0两种情况讨论存在直线的条件,再分析求解.
解答:解:∵直线y=k(x-2)+3与x轴,y轴交点的坐标分别是,A(2-
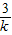
,0),B(0,3-2k).
S
△=

×|2-
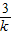
|×|3-2k|=

×
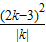
.
当k>0时,S
△=

×
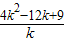
=

×(4k+
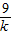
-12),
∵4k+
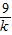
≥2
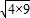
=12,当且仅当k=

时取等号.
∴当S
△=m>0时,在k>0时,k有两值;
当k<0时,S
△=

×
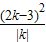
=

×
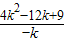
=

×[(-4k+
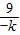
)+12],
∵-4k+
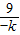
≥2
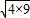
=12.当且仅当k=-

时取等号.
当m>12时,在k<0时,k有两值.;
∴当 m=0时,仅有一条直线使△AOB的面积为m,∴①不正确;
当0<m<12时,仅有两条直线使△AOB的面积为m,∴②正确;
当m=12时,仅有三条直线使△AOB的面积为m,∴③正确;
当m>12时,仅有四条直线使△AOB的面积为m,∴④正确.
故选D
点评:本题借助考查命题的真假判定,考查直线与坐标轴围成的△的面积问题.S
△的面积可根据直线在坐标轴上的截距求得.在本题中根据斜率k取值的个数来确定直线存在的条数,这是解决此类题的常用方法.

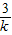 ,0),B(0,3-2k).
,0),B(0,3-2k). ×|2-
×|2-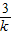 |×|3-2k|=
|×|3-2k|= ×
×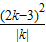 .
. ×
×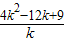 =
= ×(4k+
×(4k+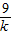 -12),
-12),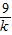 ≥2
≥2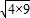 =12,当且仅当k=
=12,当且仅当k= 时取等号.
时取等号. ×
×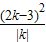 =
= ×
×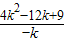 =
= ×[(-4k+
×[(-4k+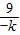 )+12],
)+12],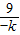 ≥2
≥2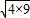 =12.当且仅当k=-
=12.当且仅当k=- 时取等号.
时取等号.

 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是