
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2a=2bcosC+csinB.
(Ⅰ)求tanB;
(Ⅱ)若C![]() ,△ABC的面积为6,求BC.
,△ABC的面积为6,求BC.
【答案】(Ⅰ)tanB=2;(Ⅱ)![]()
【解析】
(I)利用正弦定理化简已知条件,求得![]() 的值.
的值.
(II)由![]() 的值求得
的值求得![]() 的值,从而求得
的值,从而求得![]() 的值,利用正弦定理以及三角形的面积公式列方程,由此求得
的值,利用正弦定理以及三角形的面积公式列方程,由此求得![]() 也即
也即![]() 的值.
的值.
(Ⅰ)∵2a=2bcosC+csinB,利用正弦定理可得:2sinA=2sinBcosC+sinCsinB,又sinA=sin(B+C)=sinBcosC+cosBsinC,
化为:2cosB=sinB≠0,∴tanB=2.
(Ⅱ)∵tanB=2,B∈(0,π),可得sinB![]() ,cosB
,cosB![]() .
.
∴sinA=sin(B+C)=sinBcosC+cosBsinC![]() .
.
∴![]() ,可得:a
,可得:a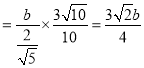 .又
.又![]() absin
absin![]() 6,可得b
6,可得b![]() .
.
∴a![]() ,即
,即![]() ,解得
,解得![]() =
=![]() .
.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源: 题型:
【题目】某高校艺术学院2019级表演专业有27人,播音主持专业9人,影视编导专业18人.某电视台综艺节目招募观众志愿者,现采用分层抽样的方法从上述三个专业的人员中选取6人作为志愿者.
(1)分别写出各专业选出的志愿者人数;
(2)将6名志愿者平均分成三组,且每组的两名同学选自不同的专业,通过适当的方式列出所有可能的结果,并求表演专业的志愿者![]() 与播音主持专业的志愿者分在一组的概率.
与播音主持专业的志愿者分在一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】请从下面三个条件中任选一个,补充在下面的横线上,并作答.
①AB⊥BC,②FC与平面ABCD所成的角为![]() ,③∠ABC
,③∠ABC![]() .
.
如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,PA⊥平面ABCD,且PA=AB=2,,PD的中点为F.
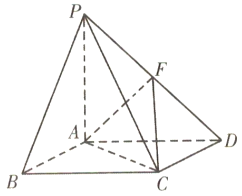
(1)在线段AB上是否存在一点G,使得AF![]() 平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
平面PCG?若存在,指出G在AB上的位置并给以证明;若不存在,请说明理由;
(2)若_______,求二面角F﹣AC﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆与![]() 轴相切于点
轴相切于点![]() ,过点
,过点![]() ,
,![]() 分别作动圆异于
分别作动圆异于![]() 轴的两切线,设两切线相交于
轴的两切线,设两切线相交于![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)过![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于不同两点
相交于不同两点![]() ,若曲线
,若曲线![]() 上存在点
上存在点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为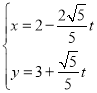 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(Ⅱ)设点![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且
上的点,且![]() .求
.求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是边长为
是边长为![]() 的等边三角形,E、F分别为AB、AC的中点,
的等边三角形,E、F分别为AB、AC的中点,![]() ,沿EF把
,沿EF把![]() 折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥
折起,使点A翻折到点P的位置,连接PB、PC,则四棱锥![]() 的外接球的表面积的最小值为________,此时四棱锥
的外接球的表面积的最小值为________,此时四棱锥![]() 的体积为________.
的体积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,
,![]()
(1)求椭圆离心率;
(2)点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求椭圆方程;
,求椭圆方程;
(3)在(2)的条件下,点![]() 在椭圆上且异于
在椭圆上且异于![]() 、
、![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,说明
,说明![]() 运动时以
运动时以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并证明.
的位置关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com