Question

函数值sin1，sin2，sin3的大小顺序是    ．

Answer 1

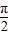
【答案】分析：根据sin2=sin（π-2），sin3=sin（π-3），而且 0＜π-3＜1＜π-2＜，函数y=sinx在（0，）上是增函数，可得sin（π-3）＜sin1＜sin（π-2），从而得出结论．
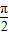
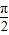
解答：解：由于sin2=sin（π-2），sin3=sin（π-3），而且 0＜π-3＜1＜π-2＜，函数y=sinx在（0，）上是增函数，
故有 sin（π-3）＜sin1＜sin（π-2），即 sin3＜sin1＜sin2，
故答案为 sin3＜sin1＜sin2．
点评：本题主要考查诱导公式、正弦函数的单调性的应用，体现了转化的数学思想，属于中档题．