
【题目】已知函数![]() ,若
,若![]()
(1)求![]() 的值,并写出函数
的值,并写出函数![]() 的最小正周期(不需证明);
的最小正周期(不需证明);
(2)是否存在正整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 内恰有
内恰有![]() 个零点?若存在,求出
个零点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A.回归直线一定过样本中心( ![]() )
)
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.两个模型中残差平方和越小的模型拟合的效果越好
D.甲、乙两个模型的R2分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
, ![]() ,
, ![]() 在圆上.
在圆上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点.
两点.
①若弦长![]() ,求直线
,求直线![]() 的方程;
的方程;
②分别过点![]() ,
, ![]() 作圆
作圆![]() 的切线,交于点
的切线,交于点![]() ,判断点
,判断点![]() 在何种图形上运动,并说明理由.
在何种图形上运动,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了研究年宣传费![]() (单位:千元)对销售量
(单位:千元)对销售量![]() (单位:吨)和年利润
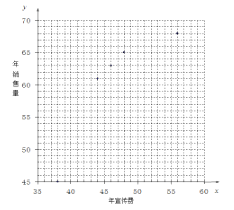
(单位:吨)和年利润![]() (单位:千元)的影响,搜集了近 8 年的年宣传费
(单位:千元)的影响,搜集了近 8 年的年宣传费![]() 和年销售量
和年销售量![]() 数据:
数据:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 38 | 40 | 44 | 46 | 48 | 50 | 52 | 56 |
| 45 | 55 | 61 | 63 | 65 | 66 | 67 | 68 |
(Ⅰ)请补齐表格中 8 组数据的散点图,并判断![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的函数表达式?(给出判断即可,不必说明理由)
的函数表达式?(给出判断即可,不必说明理由)
(Ⅱ)若(Ⅰ)中的![]() ,且产品的年利润
,且产品的年利润![]() 与
与![]() ,
, ![]() 的关系为
的关系为![]() ,为使年利润值最大,投入的年宣传费 x 应为何值?
,为使年利润值最大,投入的年宣传费 x 应为何值?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1中,∠ACB=90°,E是棱CC1上的动点,F是AB的中点,AC=BC=2,AA1=4.
(1)当E是棱CC1的中点时,求证:CF∥平面AEB1;
(2)在棱CC1上是否存在点E,使得二面角A﹣EB1﹣B的大小是45°?若存在,求出CE的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的两顶点为A,B如图,离心率为
的两顶点为A,B如图,离心率为 ![]() ,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.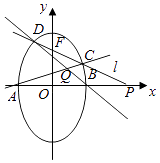
(Ⅰ)当 ![]() 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)当点P异于A,B两点时,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= ![]() .
.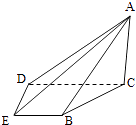
(Ⅰ)证明:AC⊥平面BCDE;
(Ⅱ)求直线AE与平面ABC所成的角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com