分析:(I)连接B1C,与BC1相交于O,连接OD,我们由三角形的中位线定理,易得OD∥AB1,进而由线面平行的判定定理得到AB1∥面BDC1;
(Ⅱ)建立如图所示的空间直角坐标系,分别求出平面C1BD和平面BDC的法向量,代入向量夹角公式,即可得到二面角C1-BD-C的余弦值;
(Ⅲ)假设侧棱AA1上存在点P,使得CP⊥面BDC1,我们可以设出P点坐标,进而构造方程组,若方程组有解说明存在,若方程组无解,说明满足条件的P点不存在.
解答:
证明:(I)连接B
1C,与BC
1相交于O,连接OD
∵BCC
1B
1是矩形,
∴O是B
1C的中点.
又D是AC的中点,
∴OD∥AB
1.(2分)
∵AB1?面BDC
1,OD?面BDC
1,
∴AB
1∥面BDC
1.(4分)
解:(II)如图,建立空间直角坐标系,则
C
1(0,0,0),B(0,3,2),C(0,3,0),A(2,3,0),
D(1,3,0)(5分)
设
=(x,y,z)是面BDC
1的一个法向量,则
即
,令x=1
则
=(1,
-,
).(6分)
易知
=(0,3,0)是面ABC的一个法向量.
∴cos<
,
>=
.(8分)
∴二面角C
1-BD-C的余弦值为
.(9分)
(III)假设侧棱AA
1上存在一点P(2,y,0)(0≤y≤3),使得CP⊥面BDC
1.
则
,即
∴方程组无解.∴假设不成立.
∴侧棱AA
1上不存在点P,使CP⊥面BDC
1.(14分)
点评:本题考查的知识点是二面角的平面角及求法,直线与平面平行的判定,直线与平面垂直的判定,其中(I)的关键是证得OD∥AB1,(II)(III)的关键是建立空间坐标系,将二面角问题和线面垂直问题转化为空间向量夹角问题.

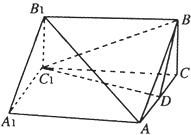 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点.
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,BC=AC=2,AA1=3,D为AC的中点. 证明:(I)连接B1C,与BC1相交于O,连接OD
证明:(I)连接B1C,与BC1相交于O,连接OD

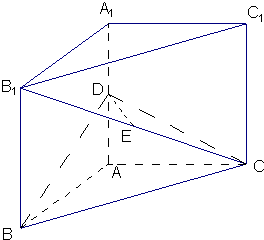 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.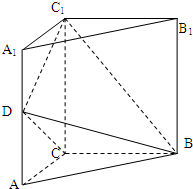 (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=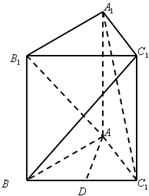 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB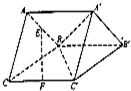 (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=