
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=45°,PD⊥平面ABCD,AP⊥BD.
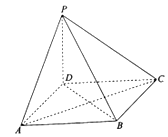
(1)证明:BC⊥平面PDB,
(2)若AB![]() ,PB与平面APD所成角为45°,求点B到平面APC的距离.
,PB与平面APD所成角为45°,求点B到平面APC的距离.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)通过证明![]() 平面
平面![]() 证得
证得![]() ,即有
,即有![]() ,结合
,结合![]() ,证得
,证得![]() 平面
平面![]() .
.
(2)利用等体积法,由![]() 列方程,解方程求得点
列方程,解方程求得点![]() 到平面
到平面![]() 的距离.
的距离.
(1)证明:∵PD⊥平面ABCD,BC在平面ABCD内,BD在平面ABCD内,
∴PD⊥BC,PD⊥BD,
又AP⊥BD,AP∩PD=P,且AP,PD均在平面APD内,
∴BD⊥平面APD,
又AD在平面APD内,
∴BD⊥AD,
又底面ABCD为平行四边形,
∴BC⊥BD,
又PD∩BD=D,且都在平面PBD内,
∴BC⊥平面PDB;
(2)由(1)知,PB与平面APD所成角即为∠BPD,故∠BPD=45°,
又AB![]() ,∠DAB=45°,
,∠DAB=45°,
∴![]() ,
,![]() ,
,
∴AP2+PC2=AC2,即AP⊥CP,
∴![]() ,
,![]() ,
,
又VP﹣ABC=VB﹣PAC,
∴![]() ,即
,即![]() ,解得
,解得![]() ,
,
即点B到平面APC的距离为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某种植物感染![]() 病毒极易导致死亡,某生物研究所为此推出了一种抗
病毒极易导致死亡,某生物研究所为此推出了一种抗![]() 病毒的制剂,现对
病毒的制剂,现对![]() 株感染了
株感染了![]() 病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:
病毒的该植株样本进行喷雾试验测试药效.测试结果分“植株死亡”和“植株存活”两个结果进行统计;并对植株吸收制剂的量(单位:![]() )进行统计规定:植株吸收在
)进行统计规定:植株吸收在![]() (包括
(包括![]() )以上为“足量”,否则为“不足量”.现对该
)以上为“足量”,否则为“不足量”.现对该![]() 株植株样本进行统计,其中“植株存活”的
株植株样本进行统计,其中“植株存活”的![]() 株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共
株,对制剂吸收量统计得下表.已知“植株存活”但“制剂吸收不足量”的植株共![]() 株.
株.
编号 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
吸收量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)完成以![]() 下列联表,并判断是否可以在犯错误概率不超过
下列联表,并判断是否可以在犯错误概率不超过![]() 的前提下,认为“植株的存活”与“制剂吸收足量”有关?
的前提下,认为“植株的存活”与“制剂吸收足量”有关?
吸收足量 | 吸收不足量 | 合计 | |
植株存活 |
| ||
植株死亡 | |||
合计 |
|
(2)若在该样本“制剂吸收不足量”的植株中随机抽取![]() 株,求这
株,求这![]() 株中恰有
株中恰有![]() 株“植株存活”的概率.
株“植株存活”的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
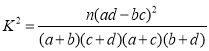 ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲乙丙丁四个人相互之间传球,从甲开始传球,甲等可能地把球传给乙丙丁中的任何一个人,依此类推.
(1)通过三次传球后,球经过乙的次数为ξ,求ξ的分布列和期望;
(2)设经过n次传球后,球落在甲手上的概率为an,
(i)求a1,a2,an;
(ii)探究:随着传球的次数足够多,球落在甲乙丙丁每个人手上的概率是否相等,并简单说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“科技引领,布局未来”科技研发是企业发展的驱动力量.2007~2018年,某企业连续12年累计研发投入达4100亿元,我们将研发投入与经营投入的比值记为研发投入占营收比,这12年间的研发投入(单位:十亿元)用图中的条形图表示,研发投入占营收比用图中的折线图表示.根据折线图和条形图,下列结论正确的有( )
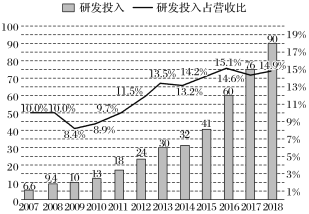
A.2012年至2013年研发投入占营收比增量相比2017年至2018年研发投入占营收比增量大
B.2013年至2014年研发投入增量相比2015年至2016年研发投入增量小
C.该企业连续12年来研发投入逐年增加
D.该企业连续12年来研发投入占营收比逐年增加
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.
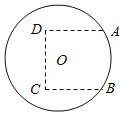
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:
①函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;
上单调递增;
②若函数![]() 在
在![]() 上有两个零点,则
上有两个零点,则![]() 的取值范围是
的取值范围是![]() ;
;
③函数![]() 在
在![]() 上单调递减;
上单调递减;
④当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() .
.
上述命题正确的是__________(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com