
 所确定的平面区域的面积为S=f(t),则S的最大值为________.
所确定的平面区域的面积为S=f(t),则S的最大值为________.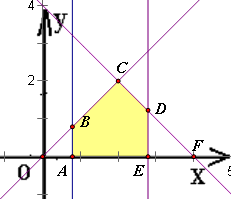 作出题中约束条件所确定的平面区域,如右图阴影部分
作出题中约束条件所确定的平面区域,如右图阴影部分 |OA|•|AB|=
|OA|•|AB|=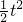 ,S△DEF=
,S△DEF= |DE|•|EF|=
|DE|•|EF|= (2-t)2,
(2-t)2, ×4×2-
×4×2-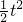 -
- (2-t)2=-t2+2t+2
(2-t)2=-t2+2t+2

科目:高中数学 来源:2012年河南省高考适应性考试数学模拟试卷(文科)(解析版) 题型:选择题
 所确定的平面区域的面积为S=f(t),则S的最大值为( )
所确定的平面区域的面积为S=f(t),则S的最大值为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com