
【题目】已知数列{xn}满足:x1=1,xn=xn+1+ln(1+xn+1)(n∈N*),证明:当n∈N*时,
(Ⅰ)0<xn+1<xn;
(Ⅱ)2xn+1﹣xn≤ ![]() ;
;
(Ⅲ) ![]() ≤xn≤
≤xn≤ ![]() .
.
【答案】解:(Ⅰ)用数学归纳法证明:xn>0,
当n=1时,x1=1>0,成立,
假设当n=k时成立,则xk>0,
那么n=k+1时,若xk+1<0,则0<xk=xk+1+ln(1+xk+1)<0,矛盾,
故xn+1>0,
因此xn>0,(n∈N*)
∴xn=xn+1+ln(1+xn+1)>xn+1 ,
因此0<xn+1<xn(n∈N*),
(Ⅱ)由xn=xn+1+ln(1+xn+1)得xnxn+1﹣4xn+1+2xn=xn+12﹣2xn+1+(xn+1+2)ln(1+xn+1),
记函数f(x)=x2﹣2x+(x+2)ln(1+x),x≥0
∴f′(x)= ![]() +ln(1+x)>0,
+ln(1+x)>0,
∴f(x)在(0,+∞)上单调递增,
∴f(x)≥f(0)=0,
因此xn+12﹣2xn+1+(xn+1+2)ln(1+xn+1)≥0,
故2xn+1﹣xn≤ ![]() ;
;
(Ⅲ)∵xn=xn+1+ln(1+xn+1)≤xn+1+xn+1=2xn+1 ,
∴xn≥ ![]() ,
,
由 ![]() ≥2xn+1﹣xn得
≥2xn+1﹣xn得 ![]() ﹣
﹣ ![]() ≥2(
≥2( ![]() ﹣
﹣ ![]() )>0,
)>0,
∴ ![]() ﹣
﹣ ![]() ≥2(
≥2( ![]() ﹣
﹣ ![]() )≥…≥2n﹣1(
)≥…≥2n﹣1( ![]() ﹣
﹣ ![]() )=2n﹣2 ,
)=2n﹣2 ,
∴xn≤ ![]() ,
,
综上所述 ![]() ≤xn≤
≤xn≤ ![]() .
.
【解析】(Ⅰ)用数学归纳法即可证明,
(Ⅱ)构造函数,利用导数判断函数的单调性,把数列问题转化为函数问题,即可证明,
(Ⅲ)由 ![]() ≥2xn+1﹣xn得
≥2xn+1﹣xn得 ![]() ﹣
﹣ ![]() ≥2(
≥2( ![]() ﹣
﹣ ![]() )>0,继续放缩即可证明
)>0,继续放缩即可证明
【考点精析】关于本题考查的利用导数研究函数的单调性和数列的通项公式,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.
在这个区间单调递减;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能得出正确答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
(a>b>0)的左、右焦点分别为F1 , F2 , 过F1且与x轴垂直的直线交椭圆于A、B两点,直线AF2与椭圆的另一个交点为C,若△ABF2的面积是△BCF2的面积的2倍,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线x2=y,点A(﹣ ![]() ,
, ![]() ),B(
),B( ![]() ,
, ![]() ),抛物线上的点P(x,y)(﹣
),抛物线上的点P(x,y)(﹣ ![]() <x<
<x< ![]() ),过点B作直线AP的垂线,垂足为Q.
),过点B作直线AP的垂线,垂足为Q.
(Ⅰ)求直线AP斜率的取值范围;
(Ⅱ)求|PA||PQ|的最大值.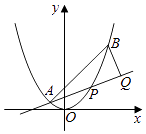
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N+),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4﹣2a1 , S11=11b4 .
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nb2n﹣1}的前n项和(n∈N+).
查看答案和解析>>
科目:高中数学 来源: 题型:
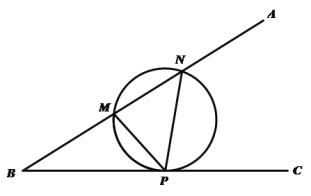
【题目】米勒问题,是指德国数学家米勒1471年向诺德尔教授提出的有趣问题:在地球表面的什么部位,一根垂直的悬杆呈现最长(即可见角最大?)米勒问题的数学模型如下:如图,设![]() 是锐角
是锐角![]() 的一边
的一边![]() 上的两定点,点
上的两定点,点![]() 是边
是边![]() 边上的一动点,则当且仅当
边上的一动点,则当且仅当![]() 的外接圆与边
的外接圆与边![]() 相切时,
相切时,![]() 最大.若
最大.若![]() ,点
,点![]() 在
在![]() 轴上,则当
轴上,则当![]() 最大时,点
最大时,点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,若数列{an}满足:an﹣k+an﹣k+1+…+an﹣1+an+1+…an+k﹣1+an+k=2kan对任意正整数n(n>k)总成立,则称数列{an}是“P(k)数列”.
(Ⅰ)证明:等差数列{an}是“P(3)数列”;
(Ⅱ)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)利用“五点法”画出函数![]() 在一个周期
在一个周期![]() 上的简图;
上的简图;
(2)先把![]() 的图象上所有点向左平移
的图象上所有点向左平移![]() 个单位长度,得到
个单位长度,得到![]() 的图象;然后把
的图象;然后把![]() 的图
的图
象上所有点的横坐标伸长到原来的2倍(纵坐标不变),得到![]() 的图象;再把
的图象;再把![]() 的图象
的图象
上所有点的纵坐标缩短到原来的![]() 倍(横坐标不变),得到
倍(横坐标不变),得到![]() 的图象,求
的图象,求![]() 的解析式.
的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣cos2x﹣2 ![]() sinx cosx(x∈R).
sinx cosx(x∈R).
(Ⅰ)求f( ![]() )的值.
)的值.
(Ⅱ)求f(x)的最小正周期及单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣ax﹣xlnx,且f(x)≥0.
(Ⅰ)求a;
(Ⅱ)证明:f(x)存在唯一的极大值点x0 , 且e﹣2<f(x0)<2﹣2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com