2或8 45°

分析:A:首先分析题目已知不等式f(x)=|x-t|+|5-x|最小值为3,求实数t的值.考虑到根据绝对值不等式的性质,绝对值之和大于等于和的绝对值.即可求出f(x)≥|5-t|,即令|5-t|等于最小值即可解得答案.
B:根据直径上的圆周角是直角、弦切角定理以及三角形内内角和定理等通过角的关系求解.
C:首先分析题目求的是直线被曲线截得弦长的问题,首先考虑题中直线是参数方程要先化为一般方程,而对于曲线是极坐标方程也要化为一般的直角坐标系方程,然后由点到直线距离公式求得圆心到直线的距离,再用勾股定理求解弦长即可.
解答:A解:因为根据绝对值不等式的性质可以得到
f(x)=|x-t|+|5-x|≥|(x-t)+(5-x)|=|5-t|
又已知f(x)=|x-t|+|5-x|最小值为3,
故有|5-t|=3,即可解出t=2或8.
故答案为:2或8.
B解:设∠EAC=α,根据弦切角定理,∠ABE=α.
根据三角形外角定理,∠AEC=90°+α.
根据三角形内角和定理,∠ACE=90°-2α.
由于CD是∠ACB的内角平分线,所以FCE=45°-α.(5分)
再根据三角形内角和定理,∠CFE=180°-(90°+α)-(45°-α)=45°.(7分)
根据对顶角定理,∠AFD=45°.
由于∠DAF=90°,所以∠ADF=45°.(10分)
故答案为:45°.
C解:将方程
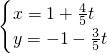
(t为参数),化为普通方程3x+4y+1=0,
将方程
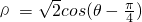
化为普通方程x
2+y
2-x-y=0,
此方程表示圆心为 (

,

),半径为

的圆.
则圆心到直线的距离
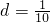
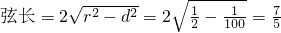
故答案为:

.
点评:A此题主要考查绝对值不等式的性质“绝对值之和大于和的绝对值”的应用,避免了分类讨论去绝对值的繁琐,有一定的技巧性,属于中档题目.
B本题的涉及很独到,试题涉及成动态的,即点C是可变的,在这个动态中求解其中的一个不变量.解决这类试题要善于抓住主要的变化关系,如本题中主要的变量就是∠AEC,抓住这个变量后,其余的角可以使用这个变量进行表达,通过各个角的关系证明求解的目标与这个变量没有关系.
C此题主要考查直线的参数方程化一般方程和圆的极坐标方程化一般方程的求法,其中应用到点到直线距离公式及勾股定理,属于综合性的试题有一定的难度.

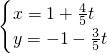 (t为参数)被曲线
(t为参数)被曲线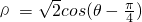 所截的弦长为________.
所截的弦长为________.
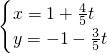 (t为参数),化为普通方程3x+4y+1=0,
(t为参数),化为普通方程3x+4y+1=0,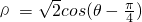 化为普通方程x2+y2-x-y=0,
化为普通方程x2+y2-x-y=0, ,
, ),半径为
),半径为  的圆.
的圆.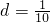
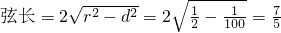
 .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(三选一,考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)