
【题目】已知函数![]() ;
;
(1)若函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,
,![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集恰好为
的解集恰好为![]() ,若存在,求出
,若存在,求出![]() ,
,![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
【答案】(1)![]() (2)存在整数
(2)存在整数![]() ,
,![]() ,
,![]() ,
,![]() 或
或![]() ,
,![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集恰好为
的解集恰好为![]()
【解析】
(1)先求出二次函数的对称轴方程,再讨论对称轴与定区间的位置关系①当![]() 时,②当
时,②当![]() 时,③
时,③![]() 时,求函数的最小值,然后运算即可得解;
时,求函数的最小值,然后运算即可得解;
(2)假设存在整数![]() ,
,![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集恰好为
的解集恰好为![]() ,即
,即![]() 的解集为
的解集为![]() ,再结合二次方程的根的关系求解即可.
,再结合二次方程的根的关系求解即可.
解:(1)函数![]() 的对称轴为
的对称轴为![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() ,不满足
,不满足![]() ,
,
②当![]() ,即
,即![]() 时,
时,![]()
![]() 符合题意.
符合题意.
③![]() ,即
,即![]() 时,
时,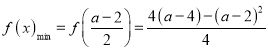
![]() .
.
综上:实数![]() 的取值范围:
的取值范围:![]() .
.
(2)假设存在整数![]() ,
,![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集恰好为
的解集恰好为![]() ,即
,即![]() 的解集为
的解集为![]() .可得
.可得![]() ,
,![]() .
.
即![]() 的两个实数根为
的两个实数根为![]() ,
,![]() .即可得出.
.即可得出.![]() ,
,![]() .
.
![]() ,当
,当![]() 时,
时,![]() 不存在,舍去,
不存在,舍去,
当![]() 时,
时,![]() ,
,![]() 或
或![]() ,
,![]() .
.
故存在整数![]() ,
,![]() ,且
,且![]() ,
,![]() 或
或![]() ,
,![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 的解集恰好为
的解集恰好为![]() .
.


科目:高中数学 来源: 题型:
【题目】下列说法中错误的是__________(填序号)
①命题“![]() ,有
,有![]() ”的否定是“
”的否定是“![]() ”,有
”,有![]() ”;
”;
②已知![]() ,
, ![]() ,
, ![]() ,则
,则![]() 的最小值为
的最小值为![]() ;
;
③设![]() ,命题“若
,命题“若![]() ,则
,则![]() ”的否命题是真命题;
”的否命题是真命题;
④已知![]() ,
, ![]() ,若命题
,若命题![]() 为真命题,则
为真命题,则![]() 的取值范围是
的取值范围是![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,某市为响应国家号召,大力推行全民健身运动,加强对市内各公共体育运动设施的维护,几年来,经统计,运动设施的使用年限x(年)和所支出的维护费用y(万元)的相关数据如图所示,根据以往资料显示y对x呈线性相关关系。

(1)求出y关于x的回归直线方程少![]()
(2)试根据(1)中求出的回归方程,预测使用年限至少为几年时,维护费用将超过100万元?
参考公式:对于一组数据(x1,yl),(x2,y2),…,(xn,Yn),其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作垂直于
作垂直于![]() 轴的直线与抛物线交于
轴的直线与抛物线交于![]() ,
,![]() 两点,且以线段
两点,且以线段![]() 为直径的圆过点
为直径的圆过点![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为曲线
为曲线![]() :
:![]() 上的动点,求
上的动点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com