
分析 根据f(x)在[a,b]上具有性质P的定义,结合函数凸凹性的性质,利用数形结合即可得到结论.
解答 解:①f(x)=$\frac{1}{x}$在[1,3]上为减函数,则由图象可知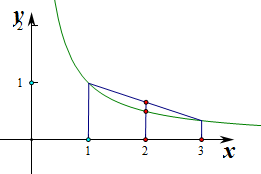 对任意x1,x2∈[1,3],有ff($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{1}{2}$[f(x1)+f(x2)]成立,故①正确:
对任意x1,x2∈[1,3],有ff($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{1}{2}$[f(x1)+f(x2)]成立,故①正确:
②不妨设f(x)=x,则对任意x1,x2∈[a,b],有f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{1}{2}$[f(x1)+f(x2)],故②不正确,
③在[1,3]上,
f(2)=f[$\frac{x+4-x}{2}$]≤$\frac{1}{2}$[f(x)+f(4-x)],
∵F(x)在x=2时取得最大值1,
∴$\left\{\begin{array}{l}{f(x)+f(4-x)≥2}\\{f(x)≤f(x)_{max}=1}\\{f(4-x)≤f(x)_{max}=1}\end{array}\right.$,
∴f(x)=1,即对任意的x∈[1,3],有f(x)=1,故③正确;
∵对任意x1,x2,x3,x4∈[1,3],
f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{1}{2}$[f(x1)+f(x2)],f($\frac{{x}_{3}+{x}_{4}}{2}$)≤$\frac{1}{2}$[f(x3)+f(x4)],
∴f($\frac{\frac{{x}_{1}+{x}_{2}}{2}+\frac{{x}_{3}+{x}_{4}}{2}}{2}$)≤$\frac{1}{2}$(f($\frac{{x}_{1}+{x}_{2}}{2}$)+f($\frac{{x}_{3}+{x}_{4}}{2}$))≤$\frac{1}{4}$[f(x1)+f(x2)+f(x3)+f(x4)];
即f($\frac{{x}_{1}+{x}_{2}+{x}_{3}+{x}_{4}}{4}$)≤$\frac{1}{4}$[f(x1)+f(x2)+f(x3)+f(x4)].故④正确;
故答案为:①③④
点评 本题是一道新定义题,实质上是考查函数的凹凸性及应用,解题的关键是理解这一性质,灵活运用这一性质,可通过举反例,以及利用数形结合是解决本题的关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | [-2,1) | D. | (-2,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\frac{7}{4}}]$ | B. | (1,2] | C. | [1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com