
【题目】已知函数![]() (
(![]() 且
且![]() )
)
(1)判断并证明![]() 的奇偶性;
的奇偶性;
(2)求使![]() 的
的![]() 的取值范围;
的取值范围;
(3)若
![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 有三个不同的零点,若存在,求出
有三个不同的零点,若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)奇函数,证明见解析;(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求函数的定义域,并判断关于原点对称,再利用奇偶性的定义,得到![]() 和
和![]() 的关系,从而得到结论.
的关系,从而得到结论.
(2)由对数函数的图象可知,要使![]() ,需分
,需分![]() 和
和![]() 两种境况讨论.
两种境况讨论.
(3)将函数![]() 的零点转化为研究函数
的零点转化为研究函数![]() 与函数
与函数![]() 图象有3个不同的交点,通过函数图象得到
图象有3个不同的交点,通过函数图象得到![]() .
.
(1)![]() 函数
函数![]() 的定义域为
的定义域为![]() 关于原点对称,
关于原点对称,
![]() ,
,
![]() 函数
函数![]() 是奇函数;
是奇函数;
(2)![]() ,即
,即![]() ,
,
即![]() ,
,
①![]() ,等价于
,等价于![]() ,等价于
,等价于![]() ,由定义域知0>
,由定义域知0>![]() .
.
故对![]() ,当
,当![]() 时有
时有![]() .
.
②对![]() ,等价于
,等价于![]() ,等价于
,等价于![]() .
.
故对![]() ,当
,当![]() 时有
时有![]() .
.
综上可得:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(3)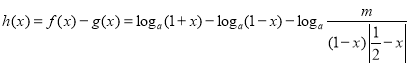 ,
,
函数![]() 有3个不同的零点
有3个不同的零点![]() 方程
方程![]() 有3个不同的根,
有3个不同的根,
由(1)知![]() 所以
所以![]()
所以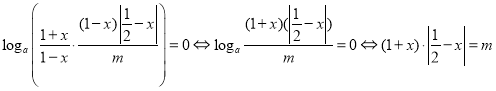 ,
,
令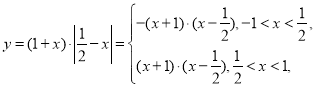 如图所示:
如图所示:
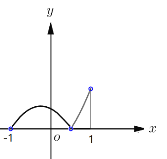
当![]() 时,
时,![]() ,
,
所以当![]() 时,函数
时,函数![]() 与函数
与函数![]() 图象有3个不同的交点,
图象有3个不同的交点,
所以当![]() 时,函数
时,函数![]() 有3个不同的零点.
有3个不同的零点.


科目:高中数学 来源: 题型:
【题目】如图,已知双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,
,![]() 是双曲线右支上的一点,
是双曲线右支上的一点,![]() 与
与![]() 轴交于点
轴交于点![]() 的内切圆在边
的内切圆在边![]() 上的切点为
上的切点为![]() ,若
,若![]() ,则双曲线的离心率是 ( )
,则双曲线的离心率是 ( )

A. 2 B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别是双曲线
分别是双曲线![]() 的左顶点、右焦点,过
的左顶点、右焦点,过![]() 的直线
的直线![]() 与
与![]() 的一条渐近线垂直且与另一条渐近线和
的一条渐近线垂直且与另一条渐近线和![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.若
两点.若![]() ,则
,则![]() 的离心率是( )
的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产一种化工产品,该产品若以每吨10万元的价格销售,每年可售出1000吨,若将该产品每吨分价格上涨![]() ,则每年的销售数量将减少
,则每年的销售数量将减少![]() ,其中m为正常数,销售的总金额为y万元.
,其中m为正常数,销售的总金额为y万元.
(1)当![]() 时,该产品每吨的价格上涨百分之几,可使销售总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售总金额最大?
(2)当![]() 时,若能使销售总金额比涨价前增加,试设定m的取值范围.
时,若能使销售总金额比涨价前增加,试设定m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往销售经验得到下面有关生产销售的统计规律:每生产产品x(百台),其总成本为g(x)(万元),其中固定成本为2万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本),销售收入R(x)(万元)满足![]() 假设该产品产销平衡,试根据上述资料
假设该产品产销平衡,试根据上述资料
(Ⅰ)要使工厂有盈利,产量x应控制在什么范围内;
(Ⅱ)工厂生产多少台产品时,可使盈利最多?
(Ⅲ)当盈利最多时,求每台产品的售价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的方程2x2﹣ax﹣2=0的两根分别为α、β(α<β),函数![]()
(1)证明f(x)在区间(α,β)上是增函数;
(2)当a为何值时,f(x)在区间[α,β]上的最大值与最小值之差最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具公司制作木质的椅子和书桌两种家具,需要木工和漆工两道工序,已知木工平均6个小时做一把椅子,10个小时做一张书桌,该公司每月木工最多有6000个工作时;漆工平均4个小时漆一把椅子,2个小时漆一张书桌,该公司每月漆工最多有2600个工作时![]() 又已知制作一把椅子和一张书桌的利润分别是15元和20元,根据以上条件,怎样安排每月的生产,才能获得最大的利润?
又已知制作一把椅子和一张书桌的利润分别是15元和20元,根据以上条件,怎样安排每月的生产,才能获得最大的利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com